Ein Tausch bedeutet immer Nehmen und Geben, so dass er mindestens zwei Teilnehmer voraussetzt. Einer von diesen Teilnehmern soll jetzt unser Milchtrinker sein. Dieser ist natürlich bestrebt, mehr Milch zu haben, aber um an sie heran zu kommen, wird er auch etwas abgeben müssen. Nehmen wir an, er ist kein Vegetarier, er isst auch Würstchen, aber er mag sie nicht besonders, so dass er unter Umständen bereit wäre auf einige von ihnen zu verzichten. Was bedeutet es aber genau, wenn wir sagen, dass er Würsten nicht so sehr mag (wie Milch)? Wie können wir uns das genauer vorstellen? Eine Möglichkeit bietet uns die Nutzenfunktion. Wenn wir nämlich die Nutzenfunktion bzw. die Nutzenkurve des Milchtrinkers in Bezug auf Würstchen in einem Diagramm darstellen, sie wird sie unter der Nutzenkurve in Bezug auf Milch liegen. So wie es das untere Bild zeigt.

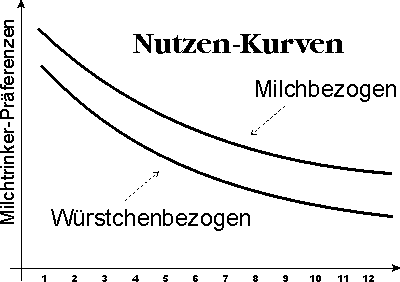
Nachdem sich der Milchtrinker entschieden hat, Würstchen gegen Milch anzubieten, wissen wir schon, dass er einen Würstchenesser für seinen Tausch finden muss. Unserem Milchtrinker ist es natürlich vollkommen egal, wer dieser Würstchenesser sein wird. Wir bleiben damit bei unserer Annahme, dass der Milchtrinker (1) ein Individualist ist, der von der Gesellschaft nichts hält und dazu noch (2) ein homo oeconomicus, der sich an keine Moral gebunden fühlt. Im ersten Schritt unserer Analyse nehmen auch an, dass der Markt für eine Milchpulverdose ein Würstchen verlangt. Nun haben wir alle Daten, die wir brauchen um herauszufinden, wie der Tausch ablaufen wird.

Wir können uns gut vorstellen, was im Kopf des kühl-rechnenden Milchtrinkers vorgeht. In seinem Besitz sind zuerst 10 Milchpulverdosen und 10 Würstchen. Eine zusätzliche, also die 11. Milchpulverdose kann er haben, wenn er auf eins, es ist bei ihm das 10. Würstchen verzichtet. (Weil alle Würstchen gleich sind, ist es völlig egal, welches das „zehnte“ sein wird.) Die Frage ist nur, ob sich für ihn ein solcher Tausch lohnen würde. Er wird sich bestimmt lohnen, weil ihm der Erwerb der 11. Milchpulverdose mehr bringt als die Verzicht auf das 10. Würstchen. Stehen uns die Nutzenkurven zur Verfügung, lässt sich ganz genau herausfinden, wie viel mehr Nutzen ein solcher Tausch bringt. Im nächsten Bild ist dieser Nettogewinn des Tausches mit grüner Farbe markiert.

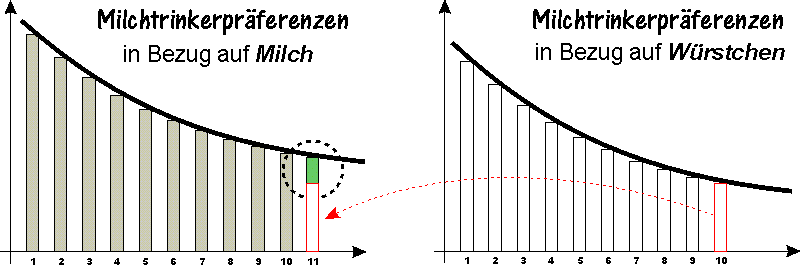
Wenn wir uns diesen Tausch genauer anschauen, können wir folgendes feststellen: Im gerade erörterten Fall sind die Nutzenwerte der (ersten) 10 Milchpulverdosen und der (ersten) 9 Würstchen ohne Belang. Würden die Nutzenwerte dieser Güter anders verlaufen, würde sich an dem Ergebnis trotzdem nichts ändern. Der Mathematiker würde sagen: Unsere Schlussfolgerungen behalten immer ihre Gültigkeit, wenn die Nutzenkurven stetige und monoton fallende Funktionen sind. Daraus schließen wir, dass beim Tausch nur die Nutzenwerte der letzten zur Verfügung stehenden Einheit eines jeden Gutes von Bedeutung sind. Anders gesagt, es sind die Nutzenwerte der Güter, die sich an der Grenze des Verbrauchs befinden. Deshalb wurde die neue mathematische Theorie treffend auch als Grenznutzentheorie bezeichnet. Dies aber nur nebenbei.

Nun hat unser Milchtrinker nach dem ersten Tausch insgesamt 11 Milchpulverdosen und 9 Würstchen. Ihm ist es möglich, sich noch eine Milchpulverdose zu verschaffen, wenn er das 9. Würstchen hergeben würde. Weil auch dieser Tausch für ihn gewinnbringend ist, wird er sich auch dafür entscheiden. Dasselbe wird er noch einmal tun, aber weiter wird er nicht gehen. Bei dieser Konstellation, um mit Hermann Gossen zu sprechen (2. Gossensches Gesetz), kommt es zum „Ausgleich des Grenznutzens“. Der Milchtrinker wird sein 7. Würstchen folglich nicht mehr tauschen wollen, um die 14. Milchpulverdose zu bekommen, weil sich damit sein Nettonutzen verringern würde. Am Ende des Tausches kämen wir also zu einem Ergebnis, so wie es das nächste Bild zeigt.

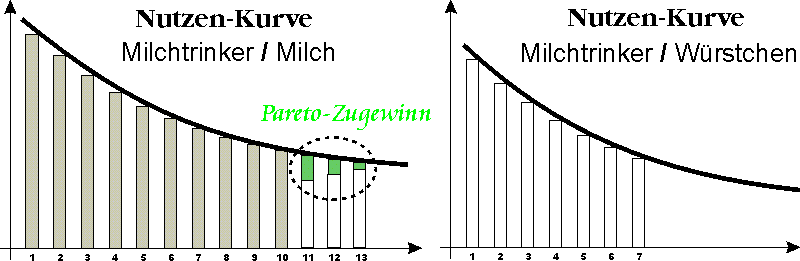
Aus dem Bild lässt sich folgern, dass sich der Milchtrinker durch den Tausch einen ordentlichen (Paretoschen) Gewinn verschafft hat, der grün dargestellt ist. Wie sieht es aber mit dem Würstchenesser aus? Weil bei ihm die Nutzenfunktionen genau umgekehrt eingeordnet sind, die Nutzenkurve für Würstchen liegt oben und die für Milch unten, wird auch er am Ende des Tausches mit einem ordentlichen (Paretoschen) Gewinn dastehen. Auch seinen Zugewinn kann man zahlenmäßig genau ausrechnen. Die Mathematik lässt uns also über den Tausch bzw. seine Gewinne etwas wissen, was ohne sie unmöglich wäre.

Es ist natürlich klar, dass sich die dargestellte Vorgehensweise auf alle Güter und zwischen allen Teilnehmern anwenden lässt. Wenn die Tauschverhältnisse bei einigen Gütern nicht so einfach sind wie vorhin (1:1), dann würde dies die Umrechnung ein bisschen verkomplizieren, aber prinzipiell wird sich damit an der Vorgehensweise nichts ändern. Wir würden ebenso zu eindeutigen Ergebnissen kommen. Wenn wir abschließend noch den Gütern richtige Preise zuweisen, etwa in €, wird sich zeigen, dass der Grenznutzen jedes Gutes pro 1 € gleich ist.

Entspricht aber diese Vorgehensweise dem, was in der Realität wirklich passiert? In gewissem Sinne schon. Wir gehen zwar in einen Laden nicht, um Güter zu tauschen, sondern wir haben Geld in der Hand und suchen uns Güter aus, so wie es unser Milchtrinker tut. Für jeden nächsten € kaufen wir das, was wir am meistens begehren. Man kann also davon ausgehen, dass es so etwas wie eine Nutzenfunktion in unserem Kopf gibt. Das haben auch die Ökonomen vor Walras nicht bezweifelt. Nichts Besonderes wäre es für sie auch, diese Funktion mathematisch darzustellen und den Tausch so zu interpretieren, wie wir es getan haben. Womit hat sich dann Walras überhaupt verdient gemacht?

Wir sind oben von der Annahme ausgegangen, dass 1 Milchpulverdose für 1 Würstchen ausgetauscht wird, aber woher hatten wir dieses Wissen? In unserem Beispiel war es so, dass wir abgewartet haben, bis der wirkliche Tausch in dem Gefangenenlager beendet ist, und dann konnten wir die Tauschwerte einfach empirisch ermitteln. Wäre dies die einzige Möglichkeit, dann ließe sich das Walrassche Modell nicht einmal ernst nehmen: es wäre völlig nutzlos. Walras hat aber gezeigt, dass wir die Tauschwerte gar nicht im Voraus wissen müssen, weil wir sie ausrechnen können. Hier wird uns erst richtig klar, was Walras geleistet hat. Er hat sein System der mathematischen Gleichungen so konzipiert, dass er von zwei Datenmengen ausgehend

• Gütermengen
• Präferenzen (Nutzenfunktionen)

als Ergebnis auch Tauschverhältnisse bzw. Preise bestimmen konnte. Dies war eigentlich seine ursprüngliche Motivation. Damit hat er bewiesen, dass die Preise der Güter ihrer Seltenheit proportional sind. (Später hat man die Ausdrucksweise präzisiert, so dass man heute sagt, der Preis entspreche dem Grenznutzen.) Rein theoretisch betrachtet, ist dies eine bewundernswerte Leistung. Was bedeutet sie aber praktisch? Um dies herauszufinden, vergleichen wir das Tauschmodell von Walras mit seinem Vorbild, also dem Modell der mechanischen Bewegung der klassischen Physik. Beide Modelle bzw. ihre mathematischen Gleichungssysteme gehen von zwei Arten von Daten aus:

Alle Größen der zweiten Datenmenge in der Mechanik, also die Kräfte, lassen sich aus den Massen und ihren Positionen (peinlich) genau ausrechen, so dass wir zu praktischen Zwecken nur die erste Datenmenge brauchen, um das reale System theoretisch vollständig zu erfassen, und dann seine „Zukunft“ auszurechnen. In der ökonomischen Theorie ist es aber nicht so, dass sich die Präferenzen aus den Gütermengen ableiten lassen. Aber wie dann?

Man kann den Standpunkt einnehmen, dass die mathematische ökonomische Theorie empirisch nicht tauglich sein muss oder gar soll. Solch eine Auffassung, also die Trennung zwischen dem Wissen und der Empirie, ist charakteristisch für die rationalistische Philosophie des kontinentalen Europa. Deshalb haben sich Walras und Pareto nicht so sehr darüber Gedanken gemacht, wozu ihre mathematischen Schlussfolgerungen („Beweise“) nützlich sein sollten. Die deutschen klassischen Philosophen haben diese stiefväterliche Verachtung der Tatsachen sogar zur höchsten Tugend der Vernunft verklärt, und die Ökonomen haben dies dankbar angenommen. Wir haben schon weit vorne Carl Menger (1840-1921) als Beispiel erwähnt, die andern sind ihm bald gefolgt: Mises, Hayek, Schumpeter, die Ordoliberalen, ... Natürlich gab es immer wieder auch Ausnahmen, die die sprichwörtliche „Regel bestätigen“. So hat etwa W. Boehmert von Anfang an und in aller Deutlichkeit auf die Untauglichkeit der neuen Theorie für irgendwelche praktische Zwecke hingewiesen. Jevons sei zwar der erste gewesen, schrieb er,

„welcher das Fundament der Volkswirtschaftslehre in die Psychologie hineingebaut habe; aber sein Versuch, Theorie und Praxis im Wege der mathematischen Methode zu vereinen, sei eine Täuschung. Seine Werttheorie sei auf den Gefühlen der Individuen aufgebaut, und diese Gefühle könnten nicht gemessen werden, weil es an der Einheit fehle, durch welche wir die Gefühle teilen könnten. Schmerz-und Lusteinheiten seien nicht vorstellbar. Der Umstand, daß der Wille in dem einen Falle so, in dem anderen so entscheide, sei in keiner Weise einer Messung zugänglich, da aus dieser Tatsache nicht der geringste quantitative Schluß gezogen werden könne.“

William Stanley Jevons (1835 - 1882), der wichtigste Pionier des Neoliberalismus im englischsprachigen Raum, hatte nicht so viel Glück wie seine kontinentalen Kollegen. Den englischen Ökonomen konnte man im 19. Jahrhundert noch nicht einfach vorgaukeln, die Realitätsfremdheit (und schon gar nicht die Realitätsfeindlichkeit) sei eigentlich eine besondere Tugend einer Theorie: der überhaupt tiefste Einblick der Vernunft in die Realität. Deshalb blieb Jevons nichts anderes übrig als immer wieder zu beteuern und zu versprechen, die mathematische (Grenznutzen-)Theorie würde sich allmählich aber ganz bestimmt zu einer empirisch relevanten Wissenschaft entwickeln. Natürlich war es ihm klar, dass er selbst nicht einmal die leiseste Vorstellung davon hat, wo man nach der Lösung suchen sollte, aber am jeden Anfang sei es nun einmal so, hatte er seine Kritiker beschwichtigt und beruhigt. Nicht anders sei es doch immer auch mit den Naturwissenschaften zu Beginn gewesen:

„Betrachten wir die Geschichte anderer Wissenschaften, so lernen wir nichts, was uns entmutigen könnte. In fast allen Fällen, in welchen jetzt genaue Messungen möglich sind, können wir auf Zeiten zurückgehen, als noch die vagsten Begriffe vorherrschend waren.

Hätten die Physiker gewartet, bis ihre Daten vollständig genau waren, bevor sie sich der Hilfe der Mathe¬matik bedienten, so wären wir noch in jenem Zeitalter der Wissenschaft, welches zur Zeit Galilei’s endete. ... Wenn wir die weniger genauen Naturwissenschaften prüfen, finden wir, daß die Physiker unten allen am kühnsten sind, ihre mathematischen Theorien vor ihren Daten zu entwickeln.“

Wie ist die Lage nach mehr als einem Jahrhundert? Man ist nirgendwo hingekommen. Man tappt immer noch auf der gleichen Stelle. Deshalb lässt sich nicht im Geringsten daran zweifeln, dass die neoliberale Theorie aus empirischer und praktischer Hinsicht von Anfang an eine Sackgasse war. Sie ist nichts, aber auch gar nichts als ein Luftschloss einiger aus der Realität geflüchteten Scharlatane, und später einer Schar zum selbstständigen Denken unfähiger Apologeten. Ihre Grundlagen, die Nutzenkurven, sind bis heute eine reine theoretische Fiktion geblieben. Wie weitsichtig bzw. raffiniert waren also die deutschen Vernunftökonomen vom Schlage „desto schlimmer für die Tatsachen“, als sie von Anfang an kategorisch darauf bestanden haben, die Theorie niemals und unter keinen Umständen auf den Boden der Tatsachen zu stellen. Sie ist wahrhaftig nicht von dieser Welt. Verzichtet man darauf, die neoliberale (Grenznutzen-)Theorie mit der üblichen Höflichkeit zu behandeln, die sie übrigens auf keinen Fall verdient, dann ist es am treffendsten, sie als eine geistige Onanie zu bezeichnen.