| |
|
 |
|
| |
| |
Der Markt ist kein Mechanismus, da der Mensch kein Kräftebündel ist |
| |
Was Ing. Walras am Gleichgewicht der Kräfte gründlich missverstanden hat |
| |
|
|
|
| |
|
Tritt eine Idee in einen hohlen Kopf, so füllt sie ihn aus - weil keine andere da ist, die ihr den Rang streitig machen könnte. |
|
| |
|
Charles-Louis Montesquieu, einer der wichtigsten Staatstheoretiker der Moderne |
|
| |
|
|
|
| |
|
Man bemüht die Mathematik für Dinge, die man ebenso gut in verständlicher Sprache präsentieren könnte - und mitunter auch für Dinge, die man in der Tat besser nicht so klar formuliert, weil sonst rasch auffallen würde, was für ein Unsinn dahinter steckt. |
|
| |
|
Paul Krugman, bekannter amerikanischer Ökonom (Nobelpreisträger, 2008) |
|
|
|
|
|
Bis zum Ende des 19. Jahrhunderts hatte ein gebildeter Mensch, der sich von der herrschenden geistigen Strömung treiben ließ, nicht die geringsten Zweifel daran, dass die Theorie von Newton die exakten Erklärungsmuster des ganzen Universums liefert. Newton hätte sozusagen den göttlichen Plan der Schöpfung entschlüsselt. In diesem Sinne bemerkte damals der französische Mathematiker und Gelehrte Joseph-Louis Lagrange in Bezug auf Newton pathetisch: „Er ist der Glücklichste, das System der Welt kann man nur einmal erfinden.“ Folglich wollte sich jede Wissenschaft, um eine „richtige“ Wissenschaft zu werden, etwas von der Physik abgucken. Seltsamerweise waren anfangs die Ökonomen diejenigen, die sich am stärksten dagegen stemmten. Ein Jahrhundert nach Smiths Tod konnte nämlich noch kein wichtiger Ökonom etwas mit der Newtonschen Mechanik anfangen. Warum diese dann am Ende des 19. Jahrhunderts doch den Kopf der liberalen Ökonomen völlig verdrehte, wird man vielleicht nie genau herausfinden können. Eine der wichtigsten Ursachen könnte die jahrzehntelange Frustration der ökonomischen Theoretiker sein. Die neue Wirtschaftsordnung wollte einfach nicht „richtig“ funktionieren. Jeder neue Aufschwung endete abrupt mit einer allgemeinen Wirtschaftskrise und einer Massenarbeitslosigkeit, für die keiner eine überzeugende Erklärung fand und schon gar nicht eine Lösung. Naive, alberne und auch recht unsinnige „Theorien“ gab es natürlich im Überfluss. So wollte z.B. der bereits erwähnte Mitbegründer des Neoliberalismus Jevons seine Zeitgenossen überzeugen, dass die ökonomischen Krisen durch Sonnenflecken verursacht werden. (Nein, das ist jetzt kein Scherz!) Bei solcher Verzweiflung kann es nicht verwundern, dass man die Hoffnung auch im Schoß der klassischen Mechanik suchte.
Hermann Gossen (1810-1858) war der erste, der sich entschied, sich mit den Federn der damaligen „Königin“ der Wissenschaften zu schmücken. Ihm fiel auf, dass die Befriedigung der Bedürfnisse eine monoton fallende Funktion ist, die als solche der mechanischen (Anziehungs-)Kraft ähnelt und als solche mit den mathematischen Mitteln der klassischen Physik interpretiert (analysiert) werden kann. Wenn ein Verbraucher zu jedem Konsumgut eine solche Funktion sozusagen im Kopfe hat, wird er seinen Verbrauchsplan so gestalten, dass der (Grenz-)Nutzen jedes von ihm gekauften Gutes pro 1 Geldeinheit gleich ist (2. Gossensches Gesetz). Der Mensch sei also ein Bündel bzw. eine Summe von festen Nutzenfunktionen, so wie jede Masse im Raum ein Bündel bzw. eine Summe von Kräften ist, die zwischen ihr und allen anderen Massen im Raum herrschen. Auf dieser Idee baut Walras sein System bzw. Modell auf. Mit seinem Modell wollte er beweisen, dass sich der Tausch zwischen zwei Individuen (und zwei Gütern) auf die Wirtschaft als Ganzes erweitern und verallgemeinern lässt. Seine Mathematik beeindruckt - dafür haben wir ihn schon gebührend gewürdigt -, ihre Ergebnisse umso weniger. Um zu „beweisen“, dass der Preis „im Prinzip“ durch die Seltenheit (Knappheit) bestimmt ist, braucht man keine dermaßen komplizierte und umständliche Theorie, weil sich so etwas aus der unmittelbaren Wahrnehmung der Tatsachen ergibt. Die Theorien sind nicht dazu da, dass man die Trivialitäten „analytisch streng“ formuliert und damit „beweist“.
Walras ging es ursprünglich vor allem um die Bestimmung der Preise, aber in der Zeit danach nutzte man sein Modell immer mehr als Beweis dafür, dass die Marktwirtschaft zum Gleichgewicht tendiert. Was ist damit gemeint?
Gleichgewicht ist auf keinen Fall ein Begriff, der aus der Wirtschaftswissenschaft stammt. Die älteren Ökonomen sprechen von Ordnung und nicht von Gleichgewicht. Der Begriff Gleichgewicht stammt natürlich aus der Mechanik. Wie schwierig es ist, diesen Begriff anders zu definieren, bestätigt uns indirekt auch ein Blick in den Duden.
Gleich|ge|wicht, das <o. Pl.> [von lat. aequilibrium, frz. équilibre]: 1. a) Zustand eines Körpers, in dem die entgegengesetzt wirkenden Kräfte einander aufheben: stabiles G.; das G. halten; sie verlor das G. und stürzte; aus dem G. kommen; die Waage ist im G.; b) Ausgeglichenheit, Ausgewogenheit, Stabilität: das europäische G.; das G. der Kräfte; Sicherung des ökologischen -s. 2. innere, seelische Ausgeglichenheit: darunter leidet mein seelisches G.; sein G. bewahren, verlieren; aus dem G. geraten; sich nicht aus dem G. bringen lassen (ruhig bleiben).
Die physikalische Deutung des Gleichgewichts kommt also im Duden an erster Stelle, sonst fällt den Linguisten nur ein, dass die seelische (psychische) Ausgeglichenheit auch als Gleichgewicht bezeichnet wird. Es ist bemerkenswert, dass im Duden nicht berücksichtigt wird, wo der Begriff Gleichgewicht am häufigsten benutzt wird, und danach seine Definition zu richten. Es ist nämlich schon längst nicht mehr die Physik, bei der das Gleichgewicht zu den wichtigsten Begriffen gehört, sondern es ist die Wirtschaftswissenschaft. Trotzdem, an die ökonomische Bedeutung des Gleichgewichtsbegiffs wagen sich die Linguisten des Duden nicht heran. Man kann sich denken warum. In der Mechanik hat der Begriff einen klaren und eindeutigen Sinn; wenn ein Ökonom über das Gleichgewicht spricht, sind auch die Spezialisten für die Sprache ratlos und verwirrt. Ist das nicht seltsam? Die Mechanik ist schon längst ein Bereich der Spezialisten, der Markt und die Wirtschaft ist dagegen etwas, womit jeder unmittelbar zu tun hat, aber die ersteren verstehen wir besser als die letzteren. Könnte es wirklich daran liegen, dass die Wirtschaft dermaßen kompliziert ist? Wir gehen dieser Frage nach.
Im Folgenden wird an einfachen Beispielen verdeutlicht, was sich die Begründer der klassischen Mechanik (Physik) unter dem Gleichgewicht vorgestellt hatten. Dann versuchen wir herauszufinden, wie die neoliberalen Ökonomen dieses Gleichgewicht verstanden haben.
Über das Gleichgewicht der mechanischen Kräfte - mit ein bisschen Humor
Der bekannteste Apfel aller Zeiten ist zweifellos der von Eva im Paradies. Auf die zweite Stelle der Rangliste kommt vermutlich der Apfel von Newton. Es wurde überliefert, Newton sei ein Apfel auf den Kopf gefallen, während er grübelnd unter einem Apfelbaum saß, der ihn auf die Idee gebracht habe, die Himmelsmechanik beruhe auf derselben Ursache wie der Fall von Äpfeln auf die Erde. Vermutlich ist diese Geschichte frei erfunden. Fachleute halten es sogar für möglich, dass Newton sie selbst erfunden hat, um nahe zu legen, dass seine Himmelsmechanik auch auf der Erde ihre Richtigkeit behält. Aber wie dem auch sei, der Newtonsche Apfel ist wirklich bestens geeignet, um eines der wichtigsten Gesetze der Mechanik zu verdeutlichen:
Kräfte treten immer paarweise auf. Übt ein Körper A auf einen anderen Körper B eine Kraft aus (actio), so wirkt eine gleichgroße, aber entgegengerichtete Kraft von Körper B auf Körper A (reactio).
Lateinischer Originaltext: Lex III. Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones is se mutuo semper esse aequales et in partes contrarias dirigi.
Dies ist natürlich das dritte Newtonsche Prinzip der Mechanik, das auch als Prinzip von Aktion und Reaktion bekannt ist. Dieses Gesetz lernte jeder von uns als Kind in der Schule. Wenn man sich aber später fachlich anders entwickelt hat, was für eine überwältigende Mehrheit gilt, kann man sich an dieses Gesetz vermutlich nicht mehr richtig erinnern, so dass uns jetzt der berühmte Apfel helfen soll, unser Gedächtnis aufzufrischen.
Suchen wir uns irgendeinen Apfel aus - es muss freilich nicht einer von denen sein, die unter dem Newtonschen Baum liegen -, halten wir ihn mit den Fingern am Stiel fest und denken nach, welche mechanischen Kräfte da im Spiel sind. Die Gravitationskraft der Erde ist bestimmt die wichtigste. Sie zieht den Apfel nach unten. Diese aktive Kraft, die wir uns als ein unsichtbares Gummiband vorstellen können, wird offensichtlich die Aktion sein. Die Muskeln in unserem Arm erzeugen eine zweite Kraft, die der Gravitationskraft genau entgegen wirkt - ihr trotzt. Diese Kraft reagiert nur: kann also in unserem Fall nur die Reaktion sein. Es leuchtet unmittelbar ein, dass die Aktion gleich der Reaktion ist, weil sich der Apfel nicht rührt. Diese einfache Überlegung bestätigt offensichtlich genau das, was das dritte Gesetz der Mechanik aussagt. Sie bringt einen Zusammenhang zum Ausdruck, der sehr einleuchtend ist.
Es wäre nicht abwegig anzunehmen, dass sich dieses Zusammenhangs schon Adam bewusst war, als ihm Eva den Apfel vor die Nase gehalten hatte, um ihn dazu zu verführen, in den Apfel zu beißen. Nehmen wir an, Adam war nicht weniger schlau als Newton, so dass auch ihm schon damals ein Zusammenhang von Aktion und Reaktion einleuchtete. Fast hatte er ihn schon als Gesetz formuliert, da geschah eine Katastrophe historischen Ausmaßes, die nicht nur die Menschheit das Paradies kostete, sondern auch die Physik viele Jahrtausende zurück warf. Nein, es ist jetzt nicht das gemeint, was Eva mit ihrem Komplizen, dem Teufel, anrichtete, sondern der Schuldige war kein anderer als der Stiel. Er erlaubte sich nämlich zu reißen und der Apfel begann zu fallen. Adams Gedanken von Aktion und Reaktion platzten in diesem Augenblick wie Seifenblasen.
Ja, wir haben im betrachteten Fall ein gewaltiges Problem mit der Newtonschen, wie er sich selber ausdrückte, Philosophie der Natur. Für das Dritte Bewegungsgesetz der Mechanik braucht man doch eine Reaktion, nicht wahr, und nun, in dem Augenblick, als sich der Apfel in Bewegung setzte, ist die Reaktion einfach weg - einfach verschwunden. Reißt also der Apfel die ganze Bewegungstheorie mit sich in den Abgrund? Ist also das Gesetz nur ein akademischer Schwindel, dem es bisher gelungen ist, sich hinter viel Mathematik erfolgreich zu verstecken?
Geben wir aber vorerst Newton eine Chance, seine Theorie zu retten. Könnte es vielleicht sein, diese geheimnisvolle Reaktion gäbe es schon, nur sie würde sich irgendwo verstecken? Also müsste man sich nur besser umschauen, dann würde man sie schon finden? Da wir aber unter Ökonomen sind, warum sollten wir nicht eine Kommission aus Wirtschaftsexperten, Wirtschaftsweisen und Ökonomieprofessoren ins Leben rufen und sie beauftragen, die Reaktion zu finden? Warum sie dazu besser geeignet sein sollten als etwa die Physiker, leuchtet sofort ein: Wie wir wissen, haben sich diese Menschen unzählige Male durch die Eigenschaft hervorgetan, etwas zu sehen, was sonst keiner sieht, und umgekehrt, wenn alle meinen etwas sehen zu können, weisen sie „analytisch streng“ nach, dass es sich dabei nur um eine Einbildung handelt. In dieser Fähigkeit sind die modernen Ökonomen so weit fortgeschritten, dass die mittelalterlichen Theologen und Mystiker vor Neid erblassen würden.
Aber lassen wir solche grausamen Vorstellungen beiseite. Natürlich haben schon die Begründer der klassischen Mechanik selber nach der Reaktion gesucht und sie auch gefunden, ohne Fachökonomen - damals gab es diese sowieso noch nicht. Sie haben sie in der Masse des Apfels gefunden. Die Masse, so ihre Antwort, widersetze sich der Anziehungskraft der Erde. Sie erzeuge eine Gegenkraft, die sich der Bewegung des Apfels entgegen stemmt.
Wie bitte? So etwas darf doch nicht ernst gemeint sein! Es ist doch widersprüchlich und unsinnig!
In der Tat ist es sehr verwirrend, der Masse die Eigenschaft zuzuschreiben, sie würde sich gegen die Gravitationskraft stemmen. Zwei Massen, in unserem Fall ist es die Masse der Erde und die Masse des Apfels, ziehen sich doch an. Dies ist schließlich der Grund, warum der Apfel auf die Erde fällt! Und nun sollen wir uns sagen lassen, die Masse des Apfels würde eine Reaktion bewirken, welche die Bewegung in Richtung Erde verhindere? Was nun? Ziehen sich die Massen an oder stoßen sie sich ab?
Wir sollten einfach annehmen, dass Masse die Eigenschaft besitzt, zwei verschiedene Arten von Kraft zu entfalten: eine anziehende und eine sich widersetzende. Die letztere bezeichnet man als Trägheitskraft. Sie ist durch die Bewegung bestimmt, so dass es sie, wenn die Masse ruht - in unserem Fall der Apfel -, nicht gibt. Die Existenz einer solchen Kraft ohne eine weitere Begründung wäre aber nicht überzeugend. Man müsste diese Kraft quantitativ präzise bestimmen und mathematisch formulieren können. Dies ist den Begründern der klassischen Mechanik auch gelungen. Die „mechanische Formel“ des fallenden Apfels sieht dann wie folgt aus:
| Aktion → g · M1 · M2 / L2 = M2 · a ← Reaktion |
|
Ist diese mathematische Gleichung auch wissenschaftlich „korrekt“? Ja, das ist sie. Verwendet man nämlich entsprechende mathematische Techniken - die zum Teil die Physiker selbst entwickelt haben -, kann man unter anderem ausrechnen, wie schnell sich der Apfel (in jedem bestimmten Augenblick) bewegen wird, wo er sich (in jedem bestimmten Augenblick) befinden wird oder welche Energie er (in jedem bestimmten Augenblick) haben wird. Eine auf den ersten Blick sinnlose und widersprüchliche Auffassung hat sich also als sehr nützlich erwiesen. Aber trotzdem, irgendwie wird man das Gefühl nicht los, dass hier etwas faul ist. Alles deutet darauf hin, dass die Reaktion, so wie wir sie gerade beschrieben haben, irgendwie doch nicht echt ist. Als ob die Reaktion nur eine spitzfindige Erfindung der Theoretiker wäre. Dies beunruhigt vor allem deshalb, weil wir gerade mit der Physik zu tun haben, die berechtigter Weise für die Königin der Wissenschaften gehalten wird. In der Physik steht doch alles auf dem festen Boden ewiger und unveränderbarer Tatsachen! Oder doch nicht? Dann schauen wir uns ein anderes Beispiel an.
Ein Bauer aus dem Ort Schilda steckt seine Axt und einen Strick in seinen Ranzen und bricht mit seinem Gaul in den nahe liegenden Wald auf. Er hat vor, einen Baum zu fällen, um sich mit dem Holz für die langen Wintertage und Winternächte zu versorgen. Nun macht er sich an die Arbeit, während sein Gaul unweit ganz unbesorgt und gemütlich weidet. Als der Baum gefällt ist, ruft der Bauer den Gaul zu sich. Dann nimmt er den vorbereiteten Strick in die Hand, ein Ende befestigt er an dem Stamm des gefällten Baums und das andere Ende am Sattel des Gauls. Dieser weiß, dass es mit seinem wohligen Weiden zu Ende geht, dass er jetzt zu schuften hat, und das gefällt ihm gar nicht. Wäre es ein ganz normales Pferd von irgendwo, würde ihm nichts übrig bleiben als zu gehorchen. Er ist aber aus dem Ort Schilda, und so einem fällt immer etwas Schlaues ein. Er redet mit ernster Miene auf den Bauern ein:
„Du meinst doch nicht wirklich, dass es in meiner Macht steht, diesen Stamm auch nur ein bisschen zu bewegen?“
Der Bauer meint zuerst, der Gaul scherze mit ihm, einfach so, und fragt zurück, warum er den Stamm nicht wegbewegen könne.
„Noch nie etwas von Physik gehört, du Bauer?“ - so der Gaul. „Wenn ich an einem Ende des Stricks ziehe, ist das die Aktion. Der Stamm am anderen Ende des Strickes wirkt dagegen, dies ist die Reaktion. Sie ist exakt so stark wie die Aktion. Es würde also gegen das physikalische Gesetz verstoßen, wenn sich dann der Stamm in Bewegung setzen würde.“
Den Bauern hat es kalt erwischt. Verschämt und rot im Gesicht kratzt sich der Bauer am Kopf, ganz verlegen schaut er ratlos um sich, dann duckt er sich und versucht ängstlich diese geheimnisvolle Reaktion irgendwo unter dem Stamm zu erblicken. Aber er sieht nichts. Dann tastet er auch mit der Hand, um sie aufzuspüren. Sie könnte nämlich auch unsichtbar sein. Aber auch diesmal bleibt er erfolglos. Er ist niedergeschlagen, aber ein stolzer Schildbürger darf doch nie nachgeben. Und in der Tat, auf einmal hebt er seinen Kopf, in seinen Augen blitzt etwas Teuflisches auf und sein Mund verzieht sich zu einem Grinsen. Er zieht die Peitsche aus seinem Sack. Dem Gaul ist klar, dass sein Theoretisieren nichts mehr nützt, und er macht sich an die Arbeit. Und siehe da, der Stamm, allen Gesetzen der Mechanik zum Trotz, bewegt sich.
Hat unser Schildbürger doch etwas übersehen, was ein Physiker nicht übersehen würde? Nein - hat er nicht. Auch ein Physiker würde unter oder hinter dem Baumstamm nichts finden. Die Reibungskraft ist nur eine Erfindung der klassischen Mechanik. Man benötig sie, um im Sinne des „Gesetzes“ von Aktion und Reaktion ein System von mathematischen Gleichungen schreiben zu können, dessen Lösungen darüber Auskunft geben wie schnell sich der Stamm (in jedem Augenblick) bewegt, wo er sich (in jedem einzelnen Augenblick) befinden wird oder wie viel Arbeit der Gaul (in jedem betrachteten Augenblick) geleistet hat. Nur dies erklärt die Theorie vom Gleichgewicht, über die Kräfte sagt sie uns gar nichts, was sich nur annähernd empirisch überprüfen ließe. Es wäre lustig, die Kräfte mit Geistern zu vergleichen, aber so abwegig wäre es nicht. In der Welt der vormodernen Menschen haben bekanntlich die bösen und die guten Geister für alles gesorgt, dann wurden sie durch die „Kräfte“ ersetzt. Gemeinsam haben sie doch etwas: Weder die Geister noch die Kräfte hat bisher jemand jemals gesehen.
Das Gleichgewicht der Kräfte ist also keine gedankliche Nachahmung dessen, was sich in der Realität „wirklich“ befindet oder abläuft. Es ist kein Spiegel der Natur. Aber man wollte das lange nicht glauben. So hat man sich auch die Gravitationskraft, also die Anziehungskraft zwischen den Planeten, als ein unsichtbares Gummiband vorgestellt und gemeint, so etwas gibt es wirklich. Deshalb kann man sich gut vorstellen, was für eine unerhörte Provokation es für die traditionellen Physiker war, als Einstein erklärte, dass die Gravitationskraft nichts mehr als nur eine Hypothese sei, eine theoretische Fiktion, die er in der Physik gar nicht brauche. Und er hat in der Tat eine bessere Theorie angeboten, als die des Gummibandes. Dieses Gummiband war also deshalb nicht sichtbar, weil es gar nicht existiert.
Das Gleichgewicht der Kräfte kann nicht real sein, und es ist auch nicht real im Sinne, dass es die Natur so abbildet, wie sie „wirklich“ - oder „an sich“ (Kant) - ist. Es ist nichts anderes als nur eine Bezeichnung, ein Name für ein theoretisches Konstrukt in der Form eines Systems von mathematischen Gleichungen, mit dessen Hilfe sich im jeden Augenblick die Koordinaten der betrachteten Partikel bestimmen lassen. Mehr ist nicht daran, aber für unsere praktischen Zwecke reicht schon dies völlig aus. Deshalb hat sich die Idee des Gleichgewichts in der Welt der mechanischen Bewegung bewährt. Nun wollen wir wissen, was die Auffassung vom Gleichgewicht in der neoliberalen Theorie bedeutet und wozu sie dort gut ist.
Das „Wesen“ und der Sinn des sog. Gleichgewichts in der neoliberalen Theorie
Das Modell des Gleichgewichts der mechanischen Kräfte beruht auf dem Prinzip, dass die (geometrische) Summe der Kräfte auf der Seite der Aktion immer gleich der (geometrischen) Summe der Kräfte auf der Seite der Reaktion ist. Dieses Gleichgewichtmodell wird immer als ein System von mathematischen Gleichungen geschrieben. Stellt ein Physiker fest, dass sich aus seinem Gleichungssystem die Positionen der berücksichtigen Partikel nicht richtig ausrechnen kann, muss er sich Gedanken machen, welche Kräfte er noch hinzufügen oder wegnehmen soll. Es hat sich aber gezeigt, dass ein solches „Basteln“ zu erstaunlich vielen und erstaunlich präzisen Ergebnissen führt. Kein Wunder also, dass der große Erfolg der Idee des Gleichgewichts ansteckend war. Auch die neuen Liberalen haben sich schließlich von der klassischen Physik verführen lassen und sind auf den Gedanken gekommen, dass der Aktion und der Reaktion in der klassischen Physik die Begriffe Angebot und Nachfrage in der ökonomischen Theorie entsprechen würden. Was sind nun Angebot und Nachfrage und wozu sollte das Konstrukt des ökonomischen Gleichgewichts gut sein?
Die Begriffe Angebot und Nachfrage sind sehr alt. Sie waren schon im vortheoretischen Zeitalter im Sprachgebrauch, also noch bevor sich das ökonomische Denken als Wissenschaft etablierte. Und sie sind sehr einfach. Wenn ein Hersteller bestimmte Güter verfertigt hat, konnte man schon immer von ihm hören, er wolle sie auf dem Markt anbieten: Seine Güter hat er folglich als Angebot bezeichnet. Das erzielte Einkommen wird er später für den Kauf bestimmter Güter ausgeben. So begibt er sich also noch einmal auf den Markt, um dort Güter seines Bedarfs nachzufragen: Das wird als Nachfrage bezeichnet. Ohne zu übertreiben lässt sich also sagen, dass das Angebot und die Nachfrage zu den trivialsten Wahrnehmungen jedes Menschen gehören, der Güter tauscht.
Warum sich die Ökonomen immer mehr für solche Trivialitäten interessieren und aus ihnen eine mathematisch monumentale Theorie des Gleichgewichts schaffen, kann nur mit dem Versagen der freien Marktwirtschaft erklärt werden. Bei den sich periodisch wiederholenden Krisen der kapitalistischen Marktwirtschaft hat man nämlich immer beobachten können, dass sie nicht durch objektive Umstände verursacht waren. Am Beginn der kapitalistischen Krise passiert nichts Ungewöhnliches, die Produktivkräfte sind vorhanden und nach wie vor intakt. Nachdem die Krise begonnen hat, hat man immer feststellen können, dass auf einmal die Produktionskräfte massenweise brach gelegt wurden und dass sich überall unverkaufte Güter stapelten. Dies ließ sich als Beweis verstehen, dass der Markt einen inneren Konstruktionsfehler hat (Sismondi Malthus). Man könnte dann im nächsten Schritt daraus das Scheitern der kapitalistischen Marktwirtschaft schließen und folglich sogar ihre Abschaffung verlangen, wie es die Sozialisten und Marx getan haben. Die Verteidiger des freien Marktes und des Kapitalismus sind also während der ökonomischen Krisen in Bedrängnis geraten. Sie mussten einen theoretischen Beweis herzaubern, mit dem sich alle Fehler des Marktes abstreiten ließen. Die Idee des bedingungslosen Gleichgewichts war nur eine der vielen, aber bei weitem die erfolgreichste.
Es gibt zwei angebotstheoretische Ansätze, wie man das Gleichgewicht in der ökonomischen Theorie deutet und damit „beweist“, warum der Nachfragemangel nicht möglich ist. Der erste ist als das Saysche „Gesetz der Absatzwege“ bekannt, für den zweiten Beweis steht natürlich das Walrassche Modell des allgemeinen Gleichgewichts.
• Das Saysche Gesetzt oder: Über die unerträgliche Leichtigkeit des ökonomischen Denkens
Ein Bild muss natürlich nicht immer mehr als Tausend Worte sagen, aber oft ist es trotzdem sehr nützlich. Deshalb verhelfen wir uns auch jetzt mit einem passenden Bild, um das Angebot und die Nachfrage zu verdeutlichen.
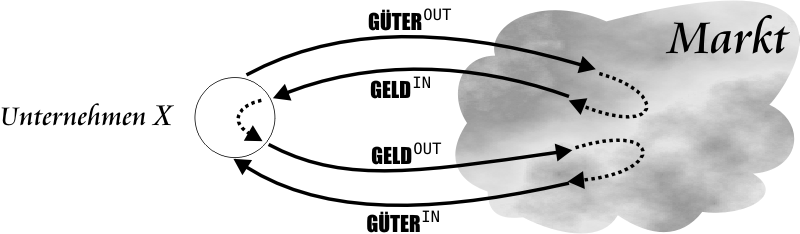
Rechts, wie eine Wolke, ist die ganze Volkswirtschaft, links wird ein Unternehmen dargestellt. Es ist ein beliebiges (X) Unternehmen, das man blindlings aus der Wirtschaft herausgegriffen und es sozusagen vergrößert hat, damit die für uns wichtigen Details besser hervorgehoben werden können. Das Unternehmen bietet eine bestimmte Gütermenge (GÜTEROUT) auf dem Markt an. Ihr Wert bzw. Preiswert, wenn sie verkauft worden sind, entspricht einer bestimmten Geldsumme (GELDIN). Diese Geldsumme wird das Unternehmen später auf dem Markt ausgeben (GELDOUT), um sich mit den Gütern seines Bedarfs zu versorgen (GÜTERIN). Dazu werden sowohl die Güter gehören, welche für die weitere Produktion nötig sind (Produktionsgüter), als auch die Konsumgüter der Beschäftigten des Unternehmens. Wenn wir die Preise der Güter mit POUT bzw. PIN bezeichnen, lassen sich diese zwei nacheinander folgenden Markttransaktionen als zwei Gleichungen schreiben.
| POUT · GÜTEROUT = GELDIN |
GELDOUT = PIN · GÜTERIN |
|
An dieser Stelle ist es angebracht, etwas über Geld zu sagen, was später auch sehr wichtig sein wird. In der Nachfragetheorie von Keynes spielt nämlich gerade das Geld die entscheidende Rolle. Keynes ist der Auffassung, dass das Unternehmen bzw. alle, die bei ihm das Einkommen bzw. das Geld beziehen, nicht ihr ganzes Einkommen bzw. Geld ausgeben. Das GELDOUT würde also nach Keynes des Öfteren kleiner sein als das GELDIN. Bei unserer Analyse des Gleichgewichts, die folgt, wollen wir dies vorerst nicht berücksichtigen. Wir bleiben bei der theoretischen Annahme, die etwa anderthalb Jahrhunderte nach Smith Tod (fast) keiner in Frage stellte, dass das ganze Geld doch vollständig ausgegeben wird. Dann kann man die letzten zwei Gleichungen als eine erweiterte Gleichung schreiben:
| POUT · GÜTEROUT = GELDIN = GELDOUT = PIN · GÜTERIN |
(1) |
Es spricht eigentlich nichts dagegen, dass man das Geld nur einmal schreibt
| POUT · GÜTEROUT = GELD = PIN · GÜTERIN |
|
oder besser noch, wir lassen das Geld ganz weg und bekommen:
| Angebot → POUT · GÜTEROUT = PIN · GÜTERIN ← Nachfrage |
(2) |
Nehmen wir jetzt an, ein Unternehmen entscheidet sich - aus welchen Gründen auch immer - die Preise der Güter (POUT), die es anbietet, zu senken. Sein in Preisen gemessenes Gesamtangebot wird sich dann natürlich verringern und damit wird auch sein Einkommen (GELDIN) schrumpfen. Folglich wird auch seine Kaufkraft (GELDOUT) entsprechend kleiner werden. Unser Unternehmen wird also, wenn die anderen Unternehmen ihre Preise nicht ändern (PIN), nicht mehr so viele Güter (GÜTERIN) auf dem Markt nachfragen bzw. kaufen wie vorher. Dem Unternehmen kann es natürlich auch gelingen, seine Preise zu erhöhen. In diesem Fall wird es dem Markt mehr abliefern, aber zugleich auch von ihm mehr abnehmen.
Wir wechseln jetzt den Standpunkt und betrachten dasselbe aus der Perspektive des Marktes. Bei niedrigeren Preisen hat der Unternehmer wertmäßig dem Markt weniger abgeliefert, aber zugleich auch weniger weggebracht. Bei höheren Preisen ist dies umgekehrt. Wichtig ist aber zu bemerken, dass ein Unternehmen - preislich betrachtet bzw. bewertet - in beiden Fällen vom Markt genau so viel wegnimmt, wie viel er ihm zuvor gegeben hat. Es hinterlässt also keine Güter auf dem Markt, die jemand anders nachfragen und wegräumen müsste. Dies lässt sich auch mathematisch gut darstellen. Man verschiebt in der letzten Gleichung das, was auf der rechten Seite steht, nach links, so dass auf der rechten Seite nur eine Null übrig bleibt.
| POUT · GÜTEROUT - PIN · GÜTERIN = 0 |
(3) |
Was für ein beliebiges Unternehmen gilt, gilt für alle. Wenn kein Unternehmer auf dem Markt etwas hinterlässt, kann sich also auf dem Markt auch nichts aufhäufen:. Der Markt wird immer geräumt. Das ist das berühmte Saysche Gesetz, das nach seinem Erfinder Jean-Baptiste Say (1767 - 1832) benannt wurde. Dieser war ein Geschäftsmann und später ein Spekulant. Als er Englisch gelernt hatte, las er auch „Wohlstand der Nationen“ von Smith, in dem er ein „riesiges Chaos richtiger Ideen, bunt durcheinandergemischt mit positiver Erkenntnis“ sah. Es lässt sich leicht erraten, was Say zu den „richtigen Ideen“ zählte: natürlich die von Smith (angeblich) uneingeschränkte Marktfreiheit. Nun wollte er diese Freiheit („unsichtbare Hand“) auf bessere theoretische Argumente stellen. Nachdem er in seiner Jugend von einem Oratorianer-Priester in Physik unterrichtet war, machte er sich auf die Suche nach unbestreitbaren, allgemeinen und fundamentalen Naturgesetzen in der Wirtschaftswissenschaft (Traité d’économie politique). Das gerade erläuterte „Gesetz der Absatzwege“ war das eine dieser „Gesetze“ - genauer gesagt das einzige. Aus ihm folgt (unter dem anderen), dass sich eine Wirtschaft im Gleichgewicht befinden muss,
- unabhängig davon, wie viele Marktakteure es gibt
- unabhängig davon, nach welchen Preisen die Güter gekauft / verkauft werden
- unabhängig davon, wie schnell sich die Preise ändern.
Wenn man diese Schlussfolgerungen verinnerlicht und sich daraus ein Gesamtbild macht, kann man kaum zu einem anderen Ergebnis gelangen, als dass das Gleichgewicht auf dem Markt eine fast unvorstellbar einfache Angelegenheit sein muss. Man kann sich dann eigentlich nicht mehr richtig vorstellen, warum eine Marktwirtschaft je aus dem Gleichgewicht geraten könnte. Wenn doch irgendwas Unerfreuliches passiert, scheint es gar nicht abwegig anzunehmen, dass dies dann auf Sinnestäuschungen und falschen Wahrnehmungen beruhen müsse. Womöglich war es auch Jevons so ergangen, als er nach den Sonnenflecken gegriffen hat, um die ökonomischen Krisen zu erklären: Wenn der Markt eine dermaßen unverwüstliche und idiotensichere Einrichtung ist, der nichts Irdisches etwas anhaben kann, könnten doch für alle Übel alleine die dunklen himmlischen Kräfte zur Verantwortung gezogen werden.
Mit Say begann man im liberalen Lager, eine ökonomische Theorie hinter dem Rücken der Tatsachen zu entwerfen. Dies war kein einfacher Kampf, weil Smith die ökonomische Theorie schon aus dem Rauch und Nebel der metaphysischen Spekulation befreit hat. Dass man diesen Kampf ein Jahrhundert nach Smith Tod trotzdem gewinnen konnte, liegt auch daran, dass Say und seine Nachfolger - wie schon hervorgehoben - keine starken Gegner hatten. Außerdem waren es nur sehr wenige. Erwähnen wir hier etwa Thomas R. Malthus (1766-1834) und Jean-Charles-Simond de Sismondi (1773-1842). Und Marx?
Für Marx war Say nur ein „fader Say“, ein Schwachkopf und ein Hampelmann, der sich mit lächerlichen Trivialitäten wichtig machen wollte. Er hat in ihm die letzte Stufe der Vulgarisierung der liberalen Theorie nach Smith gesehen. Aber weil Marx für Say nur Häme und Spott übrig hatte, sollte man daraus keine falsche Schlussfolgerung ziehen. Marx hat nämlich auch Malthus und Sismondi in die gleiche Schublade gesteckt. Ja, ihm ging es gar nie ums Gesetzt von Say. Um genauer zu sein, er hat es nicht als falsch abgelehnt. Eigentlich war Marx immer ein Angebotstheoretiker im strengsten Sinne des Wortes. Auch hier schwamm Marx in der Mitte des mainstream der geistigen Ideen seiner Zeit, Seite an Seite mit den ökonomischen Größen wie Ricardo und Mill.
• Das Walrassche Gesetz oder: Wie sich aus dem Nichts ein beachtlicher Irrsinn herbeizaubern lässt
Die Denkweise von Say war offensichtlich äußerst einfach. Er warf alle Unternehmen auf einen Haufen und gemäß der pars-pro-toto Denkweise erklärte er, dass für die ganze Volkswirtschaft exakt das gilt, was auch für jedes einzelne Unternehmen gilt. Nicht zu Unrecht sagt also der Volksmund: „Wer nichts wird, wird Wirt, und wer gar nichts wird, wird Volkswirt.“ Erst Walras fand heraus, wie man die ökonomische Theorie von ihrem schlechten Ruf think as usual befreit: Sie sollte einfach mathematisch sein! So hat Walras das, was bei Say noch so albern klingt, in eine mathematische Sprache eingekleidet. Schauen wir uns nun an, was er eigentlich geleistet hat.
Die obige Gleichung (2) gilt für ein Unternehmen. Wir können also nacheinander eine solche Gleichung für jedes einzelne Unternehmen schreiben. Dies ergibt ein mathematisches System von Gleichungen mit der Eigenschaft, dass für jede Variable unendlich vielen Lösungen möglich sind. Solch ein System von Gleichungen ergibt, mathematisch betrachtet, keinen Sinn. In der Mathematik sagt man dazu: Es ist unterbestimmt. Dem Mathematiker ist klar, dass sich in ein solches System von Gleichungen noch zusätzliche Annahmen bzw. Gleichungen integrieren lassen. Man muss sich nur entscheiden, was für welche. Sollten wir uns z.B. für das psychologische Kriterium von Gossen (die Gossensche Gesetze) entscheiden? Ja, können wir, wenn wir wollen. Da die Präferenzen monoton fallende Funktionen sind, lässt sich nun das System von Gleichungen so lösen - aus der klassischen Mechanik kennt man dies schon seit langer Zeit -, dass jede Variable nur einen einzigen numerischen Wert als Ergebnis bekommt. Bei unseren „ökonomischen“ Gleichungen würde dies konkret bedeuten, dass jedes Gut einen Preis bekommen würde. Mit diesem mathematischen Verfahren hat Walras - wie bereits erörtert -, den „endgültigen“ Beweis erbracht, was die Preise ihrem Wesen nach sind: sie würden dem (Grenz-)Nutzen entsprechen. Was man mit einem solchen Ergebnis anfangen kann, haben wir auch erörtert  . Jetzt wollen wir herausfinden, wie sich im Rahmen des Modells von Walras mathematisch das Gleichgewicht beweisen lässt: dass die Nachfrage nie kleiner als das Angebot sein kann. . Jetzt wollen wir herausfinden, wie sich im Rahmen des Modells von Walras mathematisch das Gleichgewicht beweisen lässt: dass die Nachfrage nie kleiner als das Angebot sein kann.
Auch diesmal brauchen wir uns nicht um die Mathematik zu kümmern. Wir können mit Sicherheit davon ausgehen, dass Walras und seine Nachfolger die von ihnen gewählten mathematischen Techniken fehlerfrei beherrscht haben. Deshalb wird uns allein die Idee interessieren, die diesem Beweis zugrunde liegt. Sie ist an sich ziemlich einfach, so dass sie sich mit ein wenig logischer Anstrengung gut nachvollziehen lässt. Wir wollen uns also im Folgenden auf das logische Denken verlassen. Deshalb wäre es nicht schlecht, wenn wir uns zugleich etwas in Erinnerung rufen, was wir (irgendwann früher) aus der formalen Logik gelernt oder gelesen haben.
Der syllogistische Trugschluss: Die Syllogismen bilden den Kern der im vierten vorchristlichen Jahrhundert entstandenen antiken Logik des Aristoteles und der traditionellen Logik bis ins 19. Jahrhundert. Sie sind sozusagen das ursprüngliche Muster des abendländischen Denkens, aus dem sich die moderne westliche Zivilisation entwickelt hat. Die Lehre von Syllogismen hat also große Verdienste für die Entstehung und die Herausbildung unserer Zivilisation, die ihr keiner streitig machen kann. Wegen ihren Schwächen und Fehler hat sie aber immer mehr an der Bedeutung verloren.
Unter dem Syllogismus versteht man ein Muster für Aufstellung von unmittelbaren Schlüssen. Jeweils zwei Prämissen (Voraussetzungen), Obersatz und Untersatz genannt, führen zu einer Konklusion, also zum Schlusssatz. Dies hört sich vielleicht ein bisschen kompliziert an, aber an einem bekannten Beispiel wird sofort klar, worum es geht:
| Obersatz: |
Alle Menschen sind sterblich. |
| Untersatz: |
Sokrates ist Mensch. |
|
| Schlusssatz: |
Auch Sokrates ist sterblich |
Bei genauerem Hinsehen merken wir, wo die große Schwäche dieses Schließens liegt. Sokrates, also der Mittelbegriff (terminus medius) des Untersatzes ist kein neuer Begriff in unserem Schlussfolgerungsmodell, sondern er unterliegt dem Hauptbegriff Menschen im Obersatz. Wir haben also mit einer Scheinschlussfolgerung nach dem folgenden Muster zu tun:
| Obersatz: |
Alle Menschen sind sterblich. |
| Untersatz: |
Einige Menschen sind Menschen. |
|
| Schlusssatz: |
Auch einige Menschen sind sterblich. |
So etwas sei eine „fruchtlose Scholastik“, so der Begründer bzw. Stammvater des Empirismus Francis Bacon (1561-1626). Deshalb lehnt er sie bedingungslos und restlos ab und schwört das Denken auf empirische Tatsachen ein (Novum Organum, 1620). Wie konnte es der "Wirtschaftswissenschaft" nur gelingen, sich diesem neuen Geist der Wissenschaften vom Anfang der Moderne zu entziehen? Der Walrassche Gleichgewichtsbeweis ist offensichtlich genau nach dem obigen syllogistischen Muster geschnitten. Das Saysche Gesetz besagt, dass (Obersatz:) die Wirtschaft, unabhängig davon, wie die Preise der Güter sind, immer und unbedingt im Gleichgewichts bleibt. Walras fügt hinzu, auch (Untersatz:) wenn die Preise der Seltenheit entsprechen, (Schlusssatz:) bleibe die Wirtschaft ebenfalls immer im Gleichgewicht.
Und das war’s. So hat also Walras aus einer Trivialität eine „richtige“ und „exakte“ Wissenschaft herbeigezaubert. Darauf muss man wirklich erst kommen! Aber das ist noch nicht alles. Das Beste aus der neoliberalen Werkstätte kommt noch.
Tautologie oder Leerschluss: Man bezeichnet die Schlussfolgerungen die es gar keine sind, sondern nur in einer anderen Form etwas wiederholen, als Tautologien - auf griechisch „dasselbe sagen“. Also solche ist die Tautologie auch eine Aussage, die immer wahr ist, weil sie nur eine andere Interpretation der ausgehenden Annahmen ist, die stillschweigend als wahr gelten. Man kann es auch so sagen, dass die Tautologie nur den gleichen Inhalt in einen anderen Ausdruck kleidet. Zu den bekanntesten Beispielen für eine Tautologie gehört jene aus der Parodie Der eingebildete Kranke von Molière:
| Warum schläfert Opium Menschen ein? |
|
| Opium schläfert ein, weil es eine einschläfernde Wirkung hat. |
Mit diesem Muster im Hinterkopf schauen wir uns nun Gleichung (2) an. Auf der linken Seite sind die Güter, die ein beliebiges Unternehmen verkauft, auf der rechten Seite die Güter, welche das betreffende Unternehmen von mehreren anderen Unternehmen einkauft. Wenn wir jedes dieser Unternehmen wie eine mathematische Gleichung schreiben, werden diese Güter, die vorhin auf der rechten Seite gestanden haben, auf der linken Seite stehen. Wir stellen also fest, dass in dem System von solchen Gleichungen jedes Gut zweimal vorkommt, bei einer Gleichung auf der linken und bei einer anderen Gleichung auf der rechten Seite. Um das Gesamtangebot und die Gesamtnachfrage zu ermitteln, summiert dann der Pars-pro-toto-Denker all diese Gleichungen. Die neue Gleichung hat auf der linken Seite all das, was die einzelnen Gleichungen auf der linken Seite haben, und das gilt auch für die rechte Seite. In der Mathematik benutzt man als Symbol für das Zusammenzählen den griechischen Buchstaben ∑. In einer vereinfachter Schreibweise sieht dann diese mathematische Aggregation wie folgt aus:
| Gesamtangebot → ∑ POUT · GÜTEROUT = ∑ PIN · GÜTERIN ← Gesamtnachfrage |
(4) |
Was sich dann auf der linken Seite der so mathematisch gebildeten Gleichung befindet, ist das Gesamtangebot, und auf der rechten Seite die Gesamtnachfrage der betrachteten Wirtschaft. Ein Mathematiker würde jetzt versuchen diese Gleichung zu vereinfachen. Was würde er tun?
Ihm würde sofort auffallen, dass die Preise POUT genau dieselben, wie die PIN sind. Nur der Standpunkt des Beobachters ändert sich. Einmal werden sie aus der Perspektive des Verkäufers (OUT) und andermal des Käufers (IN) wahrgenommen. Man kann also die Indizes bei den Preisen bedenkenlos weglassen, weil sie sich auf genau dasselbe beziehen. Wenn wir dies tun und zugleich die rechte Seite auf die linke verschieben, bekommen wir:
| ∑ P ( GÜTEROUT - GÜTERIN ) = 0 |
(5) |
Das ist das berühmte Gesetz von Walras, also der berühmte „analytisch strenge“ und „endgültige“ Beweis dafür, dass das Angebot immer der Nachfrage gleich ist. Null auf der rechten Seite besagt, dass es nie möglich ist, dass auf dem Markt etwas hängen bleibt - der Markt ist immer leergeräumt.
Dem Mathematiker würde sofort auffallen, dass auch die GÜTEROUT genau dieselben sind wie die GÜTERIN. Auch hier hat sich nur der Standpunkt des Beobachters geändert. Einmal werden die Güter aus der Perspektive des Verkäufers (OUT) und andermal des Käufers (IN) wahrgenommen. Man kann also auch hier die Indizes weglassen, weil sie sich auf genau dasselbe beziehen. Und dann ist die Maske gefallen. Die Variablen in den Klammern heben sich auf, so dass das Gesetz von Walras richtig implodiert - auf den Ausdruck schrumpft:
Null ist bekanntlich gleichbedeutend mit Nichts: also kein Inhalt und keine Aussage. Das Gesetz von Walras ist eine logische Aussage, deren Inhalt nichts ist. Es ist also eine perfekte Tautologie, nicht weniger perfekt wie die des Eingebildeten Kranken von Molière. Mit einem einzigen Unterschied, dass die Tautologie bei Molière in einer literarischen, die von Walras in der mathematischen Sprache verfasst ist. Man fragt sich dann, wie es Walras und seinen Nachfolgern gelungen ist, dies so lange zu verschleiern? Es hat mehrere Ursachen, über die sich diskutieren lässt. Wo aber der Trick dieser Magie liegt, lässt sich eindeutig sagen.
Schauen wir uns die Variablen GÜTEROUT und GÜTERIN noch einmal an. So wie diese Symbole geschrieben sind, unterscheiden sie sich ein wenig, so dass schon hier nicht unbedingt gleich auffallen muss, dass es sich um ein und dieselbe Größe handelt. Aber dieser Schwindel würde vielleicht noch auffliegen. Man kann aber die Güter in mehrere Gruppen aufteilen, etwa in drei Gruppen, was üblich ist, und dann jeder Gruppe, wenn sie zu GÜTEROUT gehört, eine Bezeichnung, wenn sie aber zu GÜTERIN zugeordnet ist, eine völlig andere Bezeichnung zuweisen. Ein und dasselbe „Ding“ wird also völlig anders benannt. Dann sieht das Walrassche Gesetz wie folgt aus:
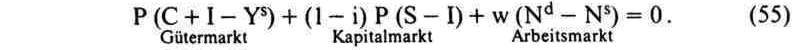 |
| . . . |
 |
| S. 76 |
Dies ist ein Auszug aus einem, unter den Studierenden ziemlich verbreiteten und beliebten Lehrbuch von Felderer und Homburg: Makroökonomik und neue Makroökonomik. Das „Gesetz“, wie oben dargestellt, ist im Grunde nichts anderes als unsere Gleichung (5) - wenn man GÜTER entsprechend zergliedert und den so geschaffenen Gruppen eigentümliche Symbole zuordnet. Was also in jedem Klammernpaar steht, sind völlig identische Größen (Mengen), einmal mit positivem und andermal mit negativem Vorzeichen. Sie heben sich auf, so dass die linke Seite der vorigen Gleichung ein inhaltliches Nichts ist. Der König ist nackt. So wie der im bekannten Märchen von Hans Christian Andersen. Seltsamer Weise ist der König von Andersen schon beim ersten öffentlichen Auftritt aufgeflogen. So ein Pech! Dem neoliberalen nackten König klatschen die Intellektuellen, Akademiker, Wirtschaftsexperten, Wirtschaftsweisen, ... schon mehr als ein Jahrhundert lang Beifall. So ein Zauber kann in der Tat nicht jedem gelingen.
Oder ist das alles „nicht so einfach“, wie es auf den (aller-)letzten Blick auszusehen mag? Lässt sich das Gesetz von Walras eventuell doch rechtfertigen? Zumindest wollen wir es versuchen. Wie bereits hervorgehoben, hat das Gesetz mit Sicherheit keine versteckten mathematischen Defekte und auch uns ist bei der Interpretation seines Beweises kein mathematischer Fehler untergelaufen. So weit, so gut. Aber könnte es sein, dass wir etwas prinzipiell falsch gemacht haben? Wir haben nämlich das Walrassche Gesetz mathematisch geprüft, aber die Wirtschaftswissenschaft ist doch kein Zweig der Mathematik. Das ist sie wirklich nicht. Aber trotzdem, dies spricht nicht dagegen, dass man die neoliberale Theorie mit dem Auge eines Mathematikers betrachtet und bewertet. Ist doch gerade die Mathematik von Anfang an der ganze Stolz dieser Theorie! Und es gilt immer noch, dass die Mathematik der wahre Garant der Richtigkeit der ganzen neoliberalen Theorie ist - eigentliche der einzige.
Diese schicksalhafte Verkoppelung der neoliberalen Theorie mit der Mathematik bzw. den ideologischen Missbrauch der Mathematik vonseiten der neoliberalen Theoretiker werden wir noch genauer untersuchen, aber vorerst übersehen wir dies, um der Gleichgewichtstheorie überhaupt eine Chance zu geben. Dem Mathematiker, der uns eben sagt, dass es den Walrassche Beweis gar nicht gäbe, dass er, rein mathematisch betrachtet, eine akademische Idiotie sei, bringen wir mit den bekannten Spruch zum schweigen: Ne sutor supra crepidam! (Schuster bleib bei deinem Leisten!)
Es lässt sich leicht sagen, dass die Wirtschaftswissenschaft nichts davon halten muss, was die Mathematik bzw. die Mathematiker über sie sagen, dass sie sich nicht den Anforderungen und Kriterien der Mathematik zu beugen braucht. Aber nach welchen soll man sie dann bewerten? Diese Frage ist gar nicht so einfach zu beantworten, und die Antworten können verschieden sein. In Anbetracht der Tatsache, dass sich die neoliberale Theorie selbst von Anfang an mit der klassischen Mechanik messen wollte, bietet sich an, dass wir ihre „Wissenschaftlichkeit“ in Bezug auf die Physik bzw. die klassische Mechanik prüfen.
Das Gleichgewicht auf dem Markt und das Gleichgewicht der mechanischen Kräfte: Ein Vergleich
Wir knüpfen jetzt an das an, was am Anfang dieses Beitrags schon gesagt worden ist. Die Kräfte in der Mechanik, so die Feststellung, gibt es in Wirklichkeit gar nicht. Sie sind unsere geistigen Konstruktionen. Für sie gilt offensichtlich das, was Kant in seiner Kritik der reinen Vernunft herausgefunden hat: Die Objekte, die wir für real halten, existieren nicht „an sich“, sondern nur „für uns“. Unser „Verstand schöpft seine Gesetze nicht aus der Natur, sondern schreibt sie dieser vor“. Diese sehr komplizierte erkenntnistheoretische Frage hat später nicht nur Philosophen immer mehr beschäftigt, sondern seit etwa einem Jahrhundert - nach dem endgültigen Zusammenbruch der Newtonschen Mechanik -, auch die Physiker. Sie sind sich heute einig, dass man sich von der jahrtausende alten Täuschung über das „reale“ Objekt endgültig verabschieden muss. Die Auffassung, dass unsere Erkenntnis ein „Spiegel der Natur“ sei, so der bekannte linke amerikanische Philosoph Richard Rorty (1979), wäre nur eine „Episode der europäischen Kulturgeschichte“. Aber ganz von der empirischen Realität ist unsere Erkenntnis doch nicht abgekoppelt. Das können wir auch aus unserer Untersuchung des Gleichgewichts der mechanischen Kräfte entnehmen. Diese sehr komplizierte erkenntnistheoretische Frage hat später nicht nur Philosophen immer mehr beschäftigt, sondern seit etwa einem Jahrhundert - nach dem endgültigen Zusammenbruch der Newtonschen Mechanik -, auch die Physiker. Sie sind sich heute einig, dass man sich von der jahrtausende alten Täuschung über das „reale“ Objekt endgültig verabschieden muss. Die Auffassung, dass unsere Erkenntnis ein „Spiegel der Natur“ sei, so der bekannte linke amerikanische Philosoph Richard Rorty (1979), wäre nur eine „Episode der europäischen Kulturgeschichte“. Aber ganz von der empirischen Realität ist unsere Erkenntnis doch nicht abgekoppelt. Das können wir auch aus unserer Untersuchung des Gleichgewichts der mechanischen Kräfte entnehmen.
Wie bereits gezeigt, die mathematischen Formulierungen der Kräfte beinhalten auch Konstanten, die man im üblichen Sinne des Wortes „real“ oder „objektiv“ verstehen kann. Aber welchen Anteil haben solche Konstanten in dem gesamten Wissen? Wenn man sich die erste Gleichung dieses Beitrags anschauet, die das Gleichgewicht der Kräfte (Aktion und Reaktion) beim fallenden Apfel erfasst, stellt man sofort fest, dass diese Konstante ziemlich unauffällig und einsam in dem ganzen Ausdruck ist. Die empirischen Komponenten bestimmen also die wissenschaftlichen Theorien nur sehr sporadisch. Deshalb spricht der Erkenntnistheoretiker Willard Quines mit Recht von einer „empirischen Unterbestimmtheit der Wissenschaft“ und vergleicht sie mit einem „von Menschen geflochtenem Netz, das nur an seinen Rändern mit der Erfahrung in Berührung steht“. Wenn man darüber mehr nachdenkt, kann man sich nicht dem Eindruck erwähren, dass die wissenschaftlichen Theorien nicht „realer“ oder „objektiver“ sind, als auch viele anderen geistigen Schöpfungen des menschlichen Geistes, wie etwa Mythen, Märchen, Gedichte oder philosophische (metaphysische) Spekulationen. Wenn man darüber mehr nachdenkt, kann man sich nicht dem Eindruck erwähren, dass die wissenschaftlichen Theorien nicht „realer“ oder „objektiver“ sind, als auch viele anderen geistigen Schöpfungen des menschlichen Geistes, wie etwa Mythen, Märchen, Gedichte oder philosophische (metaphysische) Spekulationen.
In ihrer Fähigkeit etwas vorherzusagen oder genaue Anweisungen zu geben, wie man etwas Bestimmtes realisieren soll, sind aber die wissenschaftlichen „Konstruktionen“ bzw. Theorien unvergleichbar erfolgreicher als alles andere, was der menschliche Geist je hervorbrachte. Das ist eigentlich das Faszinierende an den modernen Wissenschaften. Eine wissenschaftliche Theorie macht es uns möglich in die Zukunft zu sehen. Die Prognosen der exakten Wissenschaften sind nicht selten erstaunlich richtig und präzise. Die klassische Physik bzw. Mechanik war der erste grandiose Erfolg dieser Art. Sie stellte alles, was früher Wahrsager und Propheten meinten bewerkstelligen zu können, tief in den Schatten. Wie bereits festgestellt, mit Hilfe der Gleichungen vom Typus Aktion und Reaktion lässt sich genau ausrechnen: wie schnell sich die betrachteten Gegenstände (in jedem Augenblick) bewegen werden, wo sie sich (in jedem zukünftigen Augenblick) befinden werden, welche Energie (in jedem betrachteten Augenblick) sie besitzen und einiges mehr.
Und wie sieht es aber mit dem neoliberalen Gleichgewichtsmodell aus? Zuerst fragen wir, welche Komponenten des „Totalmodells“ sich an die Realität anlehnen. Die Preise können es mit Sicherheit nicht sein, weil das Modell gerade dazu erdacht wurde, die Preise theoretisch zu bestimmen. Und wie sieht es mit den Nutzenkurven (später Indifferenzkurven) aus, bei denen das mathematische Verfahren anfängt, mit dem die neoliberale Theorie die Preise bestimmt? Ursprünglich glaubte man noch, es würde schon jemandem einfallen, wie sich diese Kurven empirisch ermitteln lassen. Diese Hoffnung hat man aber schon längst aufgegeben. Es gibt also keine einzige Stelle in der neoliberalen Theorie, die bis zur Realität reicht. Folglich ist auch der Gleichgewichtsbeweis eine reine geistige Konstruktion.
Die neoliberale Theorie mit ihrem Modell, samt ihren Beweisen, schwebt also gänzlich in der Luft - ohne irgendwo den Boden der Wirklichkeit zu berühren. So etwas ist zwar bei den exakten Wissenschaften nicht üblich, auch bei den Sozialwissenschaften ist es nicht besonders verbreitet, aber dies alleine müsste noch kein Nachteil sein. Es spricht nämlich nichts dagegen, dass wissenschaftliche Modelle rein logisch oder mathematisch aufgebaut werden - also ohne irgendwelche empirischen „Zutaten“. Aber so oder so, müssen sie etwas über die Zukunft aussagen und diese Aussagen müssen auch stimmen. Und was leistet die neoliberale Theorie mit ihrem Gleichgewichtsbeweis in dieser Hinsicht?
Sie sagt uns, dass die Marktwirtschaft immer zum Gleichgewicht tendiert, was unter anderem bedeuten sollte, sie würde stabil funktionieren, nachhaltig wachsen, die Produktivität steigern und jedem Arbeitswilligen einen adäquaten Arbeitsplatz anbieten. Folglich sei so etwas wie Krisen und Massenarbeitslosigkeit unmöglich. Sie sagt uns also, dass gerade die größten Probleme, welche die kapitalistische Wirtschaft von Anfang an begleiten, eigentlich nicht wirklich existent sind. Was kann man über eine solche „Wissenschaft“ sagen? Eins ganz bestimmt, dass mit solchen Theorien keine ernst zu nehmende Wissenschaft vorstellbar ist. Was die neoliberalen Theoretiker bieten, ist also nicht nur für das Auge des Mathematikers, sondern auch für das des Wissenschaftlers eine akademische Idiotie.
|
|
|
| |
|
|
|
|