| |
|
 |
|
| |
| |
Über die Grundidee des neuen wirtschaftswissenschaftlichen Paradigmas |
| |
b - Das Sparen und das allgemeine Gleichgewicht der Marktwirtschaft |
| |
|
|
|
| |
|
Eine neue Theorie wird, wie Sie wissen, zunächst als widersinnig bekämpft. Dann gibt man ihre Wahrheit zu, bezeichnet sie aber als selbstverständlich und bedeutungslos. Schließlich erkennt man ihre hohe Bedeutung, und ihre frühern Gegner behaupten dann, sie hätten sie selber entdeckt. |
|
| |
|
William James, bekannter amerikanischer Psychologe und Philosoph |
|
|
|
|
|
Wir konnten mit Hilfe eines sehr einfachen Beispiels herausfinden, dass das nominale und das reale Sparen völlig unterschiedliche Größen sein können. Dies ist in der Tat ein sehr überraschendes Ergebnis. In allen ökonomischen Theorien, die auf die eine oder andere Weise immer eine Realmetaphysik der Werte sind - die Marxsche und die neoliberale Theorie sind die bekanntesten -, lässt sich nämlich dieser Unterschied analytisch nicht vermitteln. Man kennt ihn gar nicht. Nominal und real sind dort sozusagen die zwei Seiten derselben Medaille. Man kann sich also fragen, ob es überhaupt von Bedeutung ist, diese zwei Aspekte des Sparens zu unterscheiden. Ja, es ist von großer Bedeutung. Das Sparen ist eine wichtige ökonomische Größe, da es in einer sehr engen Verbindung mit dem wirtschaftlichen Wachstum steht, und dann muss es wichtig sein, es richtig zu verstehen.
Geht man also von einem falschen Verständnis des Sparens aus, dann lässt sich nicht erwarten, dass man zu einer richtigen Theorie des wirtschaftlichen Wachstums gelangen wird. Die frühliberale Theorie ist ein gutes Beispiel dafür. Sie hat die ökonomische Funktion des Sparens falsch verstanden und auch ihre Auffassung über das Wachstum und die wirtschaftliche Entwicklung hat sich als völlig falsch erwiesen. Nach dieser Theorie müsste das Sparen zu mehr Beschäftigung und zu störungsfreiem Wirtschaftswachstum führen, aber am Anfang des 19. Jahrhunderts wurde immer deutlicher, dass die freie Marktwirtschaft zu periodischen Krisen und längeren Depressionen neigt. Einige Ökonomen (Sismondi, Malthus) gingen dann so weit, dass sie das Sparen sogar zur Hauptursache des Marktversagens erklärt haben. Schließlich hat diese gegensätzliche Auffassung des Sparens die ökonomische Theorie in eine angebotsorientierte und eine nachfrageorientierte gespaltet, die sich bis heute unversöhnlich gegenüber stehen.
Die falsche frühliberale Auffassung, dass das Sparen immer nur etwas Gutes sei und an sich keine Probleme verursache, wurde später mit dem sogenannten Sayschen Gesetz begründet. Das „Gesetz“ wurde bald nach Smiths Tod von Jean-Baptiste Say (1767-1832) erfunden und es konnte sich sehr bald großer Popularität erfreuen. In der mathematischen Form - manchmal als das Walrassche Gesetz bezeichnet - ist es immer noch das wichtigste Argument eines falschen Sparverständnisses und einer falschen Wachstumstheorie. Nur einmal ist es ernsthaft in Bedrängnis geraten, nämlich nach der Großen Depression. Diese Katastrophe war das krasse Gegenteil von dem, was das Saysche Gesetz ausdrücklich behauptete, so dass es seine Glaubwürdigkeit massiv einbüßte. Keynes hat die Ursache des damaligen Versagens der Marktwirtschaft darin gesehen, dass das Geld aus dem System versickert ist. Seitdem ließ sich zumindest die universelle Gültigkeit des Sayschen Gesetzes nicht mehr aufrechterhalten. Seine Verfechter wurden gezwungen Zugeständnisse zu machen: das Geld sollte keynesianisch erklärt werden, aber für den Rest sollte weiterhin die „klassische“ ökonomische Theorie zuständig bleiben. Das Ergebnis dieses „historischen“ Kompromisses in der Wirtschaftswissenschaft ist bekannt. Ein paar Jahrzehnte nach der Großen Depression bzw. dem Zweiten Weltkrieg war die Nachfragetheorie am Ende. Alle darauf folgenden Versuche von Keynes’ Nachfolgern, sich aus dieser tödlichen Umarmung zu retten, waren erfolglos.
Dies sollte für uns eine Warnung und Mahnung sein, dass mit Geld alleine keine wirkliche nachfragetheoretische Alternative zur Angebotstheorie zu schaffen ist. Wir müssen ganz von vorne anfangen, also einen zweiten frontalen Angriff auf das Saysche Gesetz wagen. Diesmal jedoch nicht aus der Position des Geldes. Um nicht falsch verstanden zu werden, muss jetzt gleich angemerkt werden, dass dies auf keinen Fall als ein Rückzug auf die Position vor Keynes begriffen werden soll, als man in der Geldhortung keine ernsthafte Gefährdung des Gleichgewichts sehen wollte. Es wird bei uns weiterhin als unbestritten gelten, dass das Geld bzw. die Geldhortung eine ständige und gefährliche Quelle des Nachfragemangels ist. Wenn wir das Geld vorerst trotzdem beiseite schieben, soll das so verstanden werden, dass wir der Nachfragetheorie mit völlig anderen Mitteln einen Durchbruch verschaffen wollen.
Dem Sayschen Gesetz nach wäre das Ungleichgewicht in einer Wirtschaft ohne Geld unmöglich, und genau das werden wir widerlegen. Deshalb bietet sich an, dass wir zuerst etwas über das Gleichgewicht ohne Geld sagen, so wie es im Rahmen des Sayschen Gesetzes verstanden wird, und zwar an unserem Beispiel aus dem vorigen Beitrag. Dieses Beispiel hat uns zu einem besseren Verständnis des Sparens verholfen, oder genauer gesagt, wir haben mit ihm den Unterschied zwischen dem nominalen und realen Sparen erklären können, der für uns weiterhin von enormer Bedeutung sein wird. In der Fortsetzung dieser Untersuchung werden wir zur allgemeinen Gleichung des Sparens gelangen, mit der sich das Gleichgewicht und Ungleichgewicht auf eine völlig neue Weise deuten und erklären lassen.
Die partikel-mechanische Auffassung das Gleichgewichts und das Saysche Gesetz
Wir haben über das Saysche Gesetz - sowie über seine mathematisierte Darstellung, das sogenannte Walrassche Gesetz - schon ziemlich alles gesagt, was wichtig ist. Das Gesetz ist im Grunde eine sehr einfache und leicht nachvollziehbare Behauptung, dass nämlich der Wert der gesamten Produktion einer Wirtschaft, also das gesamte Angebot, genau der Summe der Einkünfte entspricht, die man bei der Realisierung dieser Produktion erhält. Die Summe dieser Einkünfte stellt die gesamte Nachfrage der Wirtschaft dar. Deshalb sollte das gesamte Angebot immer gleich der gesamten Nachfrage sein. Da sich die Werte für diese zwei Größen (Aggregate) aus unserem Beispiel leicht ermitteln lassen, können wir umgehend prüfen, ob das Saysche „Gesetz“ auf unser Beispiel mit der Landwirtschaft und den Bauern anwendbar ist.
Die Summe der Einkünfte aller Bauern, also die Nachfrage, setzt sich in unserem Beispiel aus dem Amortisationsfond (A) und den Nettoeinkünften (Ÿ) zusammen. Das Angebot ist der Gesamtwert der Ernte (Y). Mathematisch lässt sich dieser quantitative Zusammenhang wie folgt schreiben:
In unserem illustrativen Beispiel sind die zwei Seiten der Gleichung zeitlich sorgfältig getrennt, was Absicht war. Wir haben nämlich ausdrücklich verlangt, dass die Bauern nach der Ernte alle ihre Weizenmengen abliefern bzw. verkaufen. Als der ganze Weizen angesammelt worden war, bekam jeder Bauer den Gegenwert auf seinem Konto gutgeschrieben - natürlich je nach der von ihm ausgelieferten Weizenmenge. Dann wurde den Bauern frei überlassen, dass sie sich das Korn zurückkaufen: als Saatgut und natürlich für das Brotbacken. Wir haben diese Abläufe in dem vorigen Beitrag auch bildlich veranschaulicht, und zwar mit je zwei Balken für jede Reproduktionsperiode. (Die gestrichelten Balken lassen wir außer Acht.) Der erste Balken jeder Reproduktionsperiode entspricht dem gesamten Einkommen der Bauern und der zweite der zum Rückkauf vorhandenen Weizenmenge. Das Balkenpaar der Reproduktionsperiode t+1 stellen wir hier zur Veranschaulichung noch einmal dar, da wir es noch zu einem anderen Zweck brauchen werden.
| |
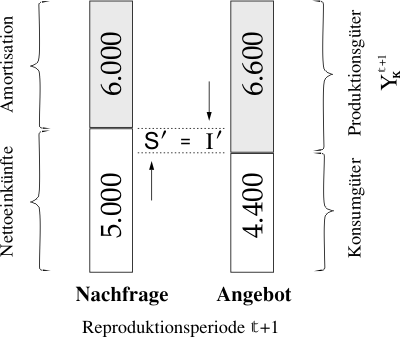 |
Die beiden Balken sind offensichtlich gleich groß. Das gilt aber nicht nur für diese Reproduktionsperiode, in der die Preise um 10% gestiegen sind. Genau dasselbe werden wir offensichtlich bei allen Reproduktionsperioden feststellen, die wir in dem vorigen Beispiel in Betracht gezogen haben. Wir können schließlich völlig dem zustimmen, was schon John S. Mill im 19. Jahrhundert bezüglich des Sayschen Gesetzes erklärt hat:
„Wenn Angebot und Nachfrage eines jeden Individuums immer einander gleich sind, dann müssen Angebot und Nachfrage aller Individuen einer Nation im Aggregat gleich sein. ... Der Beweis ist somit vollständig geführt.“
Der Beweis lässt sich tatsächlich nicht infrage stellen. Aber wurde da überhaupt etwas bewiesen? Gar nichts. Dass man mit diesem „Gesetz“ in der Praxis nichts anfangen kann, braucht man kaum zu erwähnen. Marx hat dies offensichtlich richtig gesehen, so dass er das Saysche Gesetz nicht als wirklich falsch kritisiert, sondern immer nur als eine Trivialität verspottet hat. Zu Recht. Was kann nämlich falsch bei einer Aussage sein, die eigentlich gar nichts aussagt, weil sie nur auf der Oberfläche des Phänomens verweilt? Man muss sich dann allen Ernstes fragen: Wozu das alles?.
Das kreislauftheoretische Gleichgewichtsanalyse und die allgemeine Gleichung des Sparens
Was kann man eigentlich unter einem Gesetz verstehen? Nichts anderes als eine Behauptung, dass es einen festen (quantitativen) Zusammenhang zwischen bestimmten Größen in einem Bereich der Realität gibt. Nun wollen wir herausfinden, ob sich zwischen den Größen in unserem illustrativen Beispiel neben dem Sayschen Gesetz noch irgendein quantitativer Zusammenhang finden lässt, der bei jedem Zustandekommen des Gleichgewichts seine Gültigkeit behält. Wir werden uns bei der Suche nach diesem Zusammenhang bzw. der Gesetzmäßigkeit jetzt konkreter Zahlen bedienen, die sich bei der Untersuchung der Preissteigerung am Ende des vorigen Beitrags ergeben haben. „Zurückzublättern“ müssen wir nicht, weil alle Zahlen, die wir brauchen, sich schon aus dem vorigen Bild entnehmen lassen.
Wir knüpfen jetzt an unser Beispiel aus dem vorigen Beitrag an, bei dem angenommen wurde, dass die Weizenpreise in der Reproduktionsperiode t+1 um 10% steigen. Für die Bauern bedeutete dies, dass sie für die gleiche Menge von Saatgut 10% mehr zu bezahlen hatten als früher. In unserem Bild ist diese Summe mit dem oberen Viereck des rechten Balkens dargestellt. Vergleicht man jetzt den (nominalen) Wert dieser Produktionsgüter (YKt+1) mit ihrem Wert im vorigen Jahr (YKt), dann ergibt sich eine Steigerung um 600: nämlich von 6.000 auf 6.600. Diese Steigerung (Differenz) bei den Produktionsgütern, werden wir im Folgenden mit einem Apostroph, also als YK′ darstellen. Weil wir angenommen haben, dass die Bauern auch nach der Preissteigerung alle ihre Felder so wie früher bestellen wollen, werden sie die Summe von 600 nur aus ihren Nettoeinkünften absondern können. Anders gesagt: Sie werden sie einsparen müssen. Wir bezeichnen den Wert dieser nominalen Ersparnisse mit dem Symbol S′. Nun konnten die Bauern im Oktober ihre Felder bestellen. Bei solchen Vorgängen spricht man üblicherweise von investieren. Den nominalen Zuwachs an Investitionen, der in unserem Fall 600 beträgt - siehe das vorige Bild -, bezeichnen wir mit dem Symbol I′. Zur besseren Übersicht ordnen wir jetzt alle diese Werte in eine Tabelle ein:
|
|
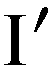 |
 |
|
600 |
600 |
600 |
Die Werte aller drei Größen (Variablen) sind gleich. Dies verleitet uns zu einer Schlussfolgerung - also zu einer „Gesetzmäßigkeit“ -, die sehr offensichtlich ist, aber wir wollen vorerst vorsichtig und zögerlich sein. Man könnte nämlich auch denken, dass der Zusammenhang zwischen diesen Größen ganz zufällig so ist, wie er ist. Deshalb versuchen wir es mit anderen Zahlen noch einmal, um dies zu prüfen.
Nehmen wir jetzt an, die Preise in unserem Beispiel würden in der Reproduktionsperiode t+1 nicht steigen, sondern fallen. Lassen wir diesmal die Preise nur um 5% fallen, weil die Preissenkungen in der Praxis erfahrungsgemäß nicht so intensiv ausfallen wie die Preissteigerungen.
Aus dem Bild lassen sich die Werte für alle drei vorhin betrachteten Größen (Variablen) schnell herausfinden:
|
|
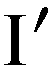 |
 |
|
-300 |
-300 |
-300 |
Es mag auf den ersten Blick überraschen, dass man negative Zahlen bekommen hat. Kann das Sparen denn negativ sein? Gewiss. Dies würde nur bedeuten, dass die Ausgaben der Bauern für den Konsum größer sind als ihre Nettoeinkünfte. Aus dem obigen Bild ist klar ersichtlich, dass die zusätzlichen Konsumausgaben aus der Amortisation stammen. Da drängt sich somit die Frage auf, ob die Bauern Probleme damit hatten, negativ zu sparen, also zu „entsparen“. Aber warum sollten sie?
Die real gleichen gesamten Investitionen (Saatgut) wie im Vorjahr (t) kosten diesmal (t+1) nominal weniger, so dass es für die Bauern sogar selbstverständlich wäre, den Rest der Amortisation für den Konsum auszugeben. Sie würden dadurch schließlich nur das real Gleiche konsumieren wie in den vorigen Jahren (Reproduktionsperioden). Wenn die Wirtschaft im Gleichgewicht bleiben soll, müssen die Bauern sogar so vorgehen. Würden sie nämlich nicht entsparen, dann ließen sich nicht alle angebotenen Konsumgüter nachfragen bzw. absetzen. Wenn sich nun noch einmal ein Zusammenhang zwischen den obigen drei Größen bestätigt hat, soll das bedeuten, dass die Übereinstimmung dieser Größen eine allgemeine Gleichgewichtsbedingung der Marktwirtschaft darstellt?
Dies anhand von nur zwei numerischen Beispielen mit ja zu beantworten, würde immer noch einen gewissen theoretischen Mut verlangen. Aber trotzdem ist dies eine richtige Schlussfolgerung, wie wir später mit besseren analytischen Mitteln nachweisen werden. Wir nehmen jetzt diesen Beweis vorweg und behaupten, dass die Übereinstimmung zwischen diesen drei Größen wirklich die allgemeine Gleichgewichtsbedingung der (freien) Marktwirtschaft darstellt. Mathematisch geschrieben:
|
|
| YK′ : |
Produktionszuwachs von Produktionsgütern
(Rohstoffe, Halberzeugnisse und Maschinen) |
| I′ : |
Nettoinvestitionen |
| S′ : |
Nettoersparnisse |
|
Ich nenne diese Gleichung allgemeine Gleichung des Sparens. Da sie noch richtig bewiesen werden muss, wollen wir jetzt über sie nicht viele Gedanken verlieren. Wir beschränken uns nur auf das, was schon jetzt ziemlich offensichtlich ist. Die rechte Seite der Gleichung, die mit den Größen I′ und S′, erfasst nämlich die Bedingung des Gleichgewichts so, wie sie in der Angebotstheorie und auch in der monetären Nachfragetheorie verstanden wird - so wie sie jeder Student am Anfang seines Studiums lernt. Sie reicht bei uns aber nicht für das allgemeine Gleichgewicht aus. Deshalb werden wir diese Identität zwischen den Größen I′ und S′ als spezielle Bedingung des Gleichgewichts bezeichnen. Erst wenn wir auch die Größe ganz links, also YK′, in Betracht ziehen, werden alle Faktoren berücksichtigt, die das Gleichgewicht der Marktwirtschaft bestimmen. Erst dann können wir von einer allgemeinen Gleichgewichtsbedingung sprechen. Das folgende Bild sollte dies veranschaulichen.
| |
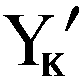 |
= |
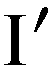 |
= |
 |
| |
|
|
| |
|
spezielle Gleichgewichtsbedingung |
|
|
| allgeimeine Gleichgewichtsbedingung |
|
Bemerkung:
Die Faktoren, welche die Investitionen (I′) und das Sparen (S′) bestimmen, werden uns in den folgenden Beiträgen nur wenig interessieren - das gehört vornehmlich zum Bereich der monetären Nachfragetheorie -, desto mehr aber diejenigen, welche die Größe YK′ bestimmen. Zu einem dieser Faktoren gehört auch die bereits untersuchte:
Hinzu werden noch
- Produktivitätswachstum und
- Wachstum
kommen, die folglich das allgemeine Gleichgewicht der Marktwirtschaft auch entscheidend bestimmen. Man kann sich gut vorstellen, dass die Gleichgewichtsanalyse damit komplizierter sein wird. Deshalb werden wir den Faktor Preisniveau immer dort, wo es geht, bevorzugen. Der Faktor Preisänderung reicht auf jeden Fall aus, die wichtigsten paradigmaspezifischen Intentionen und Grundlagen der realen Nachfragetheorie zu erklären, und zwar so, dass diese Erklärung auch dem interessierten Leser - der kein Fachmann auf diesem Gebiet ist - zugänglich ist. |
|
Es ist ein bisschen erstaunlich, wie weit wir mit Hilfe eines äußerst einfachen Beispiels gekommen sind. Dies überrascht desto mehr, wenn man bedenkt, dass Walras und Pareto mit einem ordentlichen Haufen von Mathematik nicht weiter gekommen sind, als nur zu bestätigen („nachzuweisen“), dass das Saysche Gesetz „wirklich“ in Ordnung sein sollte. Das ist in der Tat nicht berauschend viel. Aber auch uns wird es nicht gelingen, aus diesem einfachen Beispiel mehr herauszuholen, als die bereits gewonnenen Schlussfolgerungen. Sie sind sozusagen schon ziemlich alles, was die Schultern unserer Bauern aushalten konnten. Eigentlich mussten wir den Bauern schon jetzt ein bisschen unter die Arme greifen. Wir haben nämlich bei unserem Beispiel ziemlich seltsame Annahmen nötig gehabt: Die Ernte musste zuerst vollständig an eine gemeinsame Stelle (einen Quasimarkt) abgeliefert werden, die Erlöse sollten dann den Bauern auf ihre Konten gutgeschrieben werden, von denen diese sich schließlich den eigenen Weizen zurückkaufen konnten. Bei dermaßen überspannten Annahmen konnte man in der Tat berechtigte Zweifel an der allgemeinen Gleichung des Sparens bekommen. Wir brauchen in der Tat viel stärkere analytischen Mitteln - abschließend auch eine gebührende Dosis von („reiner“) Mathematik -, um sie theoretisch richtig abzusichern. Deshalb werden wir die angefangene Untersuchung in den folgenden Beiträgen ohne sie fortsetzen müssen. Wir werden diese Beiträge dem Haupttitel unterordnen, der so heißen wird wie der Titel dieses Beitrags, also:
B - Das Sparen und das allgemeine Gleichgewicht der Marktwirtschaft
Uns wird es zuerst darum gehen, zu zeigen und nachzuweisen, dass die allgemeine Gleichung des Sparens wirklich in allen Situationen und allen Umständen der realen Wirtschaft uneingeschränkt ihre Gültigkeit behält: unter anderem bei den Preisänderungen, dem Produktivitätswachstum und dem Wachstum. Wenn man es so sehen will, die allgemeine Gleichung des Sparens sollte das Saysche bzw. Walrassche Gesetzt vollständig ersetzen, was zugleich bedeuten würde, das neoliberale partikel-mechanische Modell durch das kreislauftheoretische Modell zu ersetzen und es zur Grundlage der ökonomischen Analyse zu machen. Nachdem wir die allgemeine Gleichung des Sparens bewiesen haben, werden wir den Sinn des Nachfragemangels erklären und schließlich unsere theoretischen Ergebnisse mit den empirischen Daten belegen. Mit diesen Erkenntnissen ausgerüstet werden wir uns nächsten Aufgaben widmen können: der Erklärung der zyklischen Krisen und der praktischen Wirtschaftspolitik. Dies aber nicht mehr in diesem thematischen Bereich, sondern in den folgenden.
|
|
|
| |
|
|
|
|