| |
|
 |
|
| |
| |
B - Das Sparen und das allgemeine Gleichgewicht der Marktwirtschaft |
| |
Die allgemeine Gleichung des Sparens und das (extensive) Wirtschaftswachstum |
| |
|
|
|
| |
|
Wirtschaftswachstum lässt sich nach extensiven und intensiven Wachstum unterscheiden. Extensives Wachstum findet statt, wenn die prozentuale Zunahme des Bruttoinlandsprodukts der prozentualen Zunahme der Bevölkerung entspricht. Von intensivem Wachstum wird gesprochen, wenn die prozentuale Zunahme des Bruttoinlandprodukts größer als die prozentuale Zunahme der Bevölkerung ist. |
|
| |
|
Glossar der Ökonomie |
|
|
|
|
|
Vereinfacht ausgedrückt, versteht man unter dem extensiven Wachstum eine Steigerung der realen Produktion ohne Produktivitätswachstum. Ein solches Wachstum ist für die kapitalistische Wirtschaftsordnung nicht charakteristisch und sie war immer ziemlich unfähig es zu realisieren. Langfristig betrachtet kann man sagen, dass die kapitalistische Wirtschaft fortlaufend(„tendenziell“) die Produktivität steigert - wie es Marx und Schumpeter richtig erkannt haben -, mit dem extensiven Wachstum geht es bei ihr abwechselnd bergauf und bergab. Bei den anderen Wirtschaftsordnungen war es ziemlich umgekehrt. Sie waren unfähig, nachhaltig die Produktivität zu steigern, aber viel erfolgreicher bei dem extensiven Wachstum. So etwas wie die ökonomischen Zyklen waren für sie nahezu unbekannt.
Der Vollständigkeit halber erwähnen wir nur noch kurz, dass eine Wirtschaft auch dann stagnieren kann - also nicht wachsen muss -, wenn sich die Produktionsmethoden entwickeln und die Betriebe innovativ sind. Dies kann in der kapitalistischen Wirtschaft dann der Fall sein, wenn etwa die Löhne tendenziell sinken, was wir schon analysiert haben, oder wenn sich die natürlichen Bedingungen verschlechtern - also bei der gleichzeitigen Erschöpfung der Ressourcenquellen und Umweltzerstörung. Damit wollen wir jedoch unsere weitere Untersuchung nicht belasten. Wir werden im Folgenden unter dem extensiven Wachstum ein Wachstum verstehen, bei dem die Produktionsmethoden aller Sektoren der Wirtschaft unverändert bleiben und mit gleicher Effizienz produzieren (konstante Skalenerträge). Auch diesmal wollen wir von unserem dreisektoralen Kreislaufmodell - mit dem wir uns schon vertraut gemacht haben - ausgehen. Das (extensive) Wachstum wird dann konkret bedeuten, dass die produktionstechnische Struktur unverändert bleibt - dass sich die distributiven und technischen Koeffizienten nicht ändern -, aber die Produktion steigt, und zwar bei allen Sektoren gleichmäßig (linear).
oder wenn sich die natürlichen Bedingungen verschlechtern - also bei der gleichzeitigen Erschöpfung der Ressourcenquellen und Umweltzerstörung. Damit wollen wir jedoch unsere weitere Untersuchung nicht belasten. Wir werden im Folgenden unter dem extensiven Wachstum ein Wachstum verstehen, bei dem die Produktionsmethoden aller Sektoren der Wirtschaft unverändert bleiben und mit gleicher Effizienz produzieren (konstante Skalenerträge). Auch diesmal wollen wir von unserem dreisektoralen Kreislaufmodell - mit dem wir uns schon vertraut gemacht haben - ausgehen. Das (extensive) Wachstum wird dann konkret bedeuten, dass die produktionstechnische Struktur unverändert bleibt - dass sich die distributiven und technischen Koeffizienten nicht ändern -, aber die Produktion steigt, und zwar bei allen Sektoren gleichmäßig (linear).
Man könnte annehmen, dass sich ein extensives Wachstum mit immer gleichen Produktionsmethoden analytisch am einfachsten untersuchen lässt. Sollte dies stimmen, dann hätten wir in diesem thematischen Bereich unsere Untersuchung des allgemeinen Gleichgewichts mit dem extensiven Wachstum anfangen, und sie dann mit arbeits- und kapitalsparenden Innovationen fortsetzen sollen. Wir sind aber nicht so vorgegangen, und zwar aus gutem Grund. Es mag verwirren, aber gerade das extensive Wachstum, das sich auf den ersten Blick so einfach anmutet, ist ein analytisch sehr komplexer Fall. Genauer gesprochen, betrifft dies den Übergang der Wirtschaft aus dem stationären Zustand - was etwa dem Nullwachstum in der Praxis entspricht - zum Wachstum. Eine stationäre Wirtschaft kann nämlich nicht ohne weiteres anfangen zu wachsen und dabei im Gleichgewicht bleiben. Diese dermaßen ungewöhnliche und merkwürdige Behauptung muss natürlich erst bewiesen werden. Das werden wir natürlich auch tun, aber in diesem Beitrag muss es nicht sein. Das angedeutete Übergangsproblem lässt sich einfach umgehen, ohne dass dies unserer Untersuchung des extensiven Wachstums einen Abbruch tun würde, und so werden wir auch vorgehen.
Was die Problematik des Übergangs betrifft, kann noch hinzugefügt werden, dass es sich um einen sehr interessanten Fall handelt. An ihm lässt sich nämlich am einfachsten erklären, was der Nachfragemangel in der realen Nachfragetheorie bedeutet. Diese Problematik werden wir schon in einem der nächsten Beiträge behandeln. Später, wenn wir uns im neuen thematischen Bereich den ökonomischen Zyklen widmen, werden wir noch einmal auf diese Problematik des Übergangs zurückkommen.
Die Aussage bzw. die Behauptung, dass eine stationäre Wirtschaft nicht zu wachsen beginnen kann, darf jedoch nicht so verstanden werden, dass dies überhaupt nicht möglich ist. Das ist unter bestimmten Bedingungen durchaus möglich, die sogar in der Praxis immer wieder vorhanden sind. Eine solche Bedingung wäre die Öffnung neuer Märkte im Ausland, die dann die fehlende Nachfrage übernehmen würden. Eine andere Möglichkeit wäre die von Schumpeter vorgeschlagene, dass nämlich die neuen Investitionen durch Kredite bzw. durch Geldschöpfung der Banken finanziert werden. Rein theoretisch betrachtet kann das Wachstum ohne Gleichgewichtsprobleme auch dann problemlos beginnen, wenn die Preise (der Produktionsgüter) steigen. Aber dieser Fall - wie wir noch sehen werden - kommt empirisch nicht sehr oft vor, so dass wir ihn auch theoretisch nicht in den Vordergrund stellen sollten. Dann bleibt uns nur eine Möglichkeit übrig, die Wirtschaft durch Produktivitätswachstum auf den Wachstumspfad zu hieven. Es hat sogar zwei Vorteile, die gleichgewichtstheoretische Untersuchung des Wachstums gerade mit dem Produktivitätswachstum bzw. mit Innovationen anzufangen. Wie bereits hervorgehoben, handelt es sich bei den Innovationen um eine besonders charakteristische Erscheinung in der kapitalistischen Wirtschaft. Wir haben sie vorhin untersucht, was uns jetzt sehr zugunsten kommt. Dort haben wir herausgefunden, dass eine Wirtschaft, der Innovationen zur Verfügung stehen, keine zusätzliche Nachfrage benötigt, um zu beginnen zu wachsen. Wir werden also im Folgenden die Wirtschaft durch Innovationen auf den Wachstumspfad hieven und sie dann weiter extensiv wachsen lassen. Aber bevor wir damit anfangen, sollten wir noch ein wichtiges Problem des Wachstums besprechen.
Das strukturelle bzw. produktionstechnische Problem des (extensiven) Wirtschaftswachstums
Man darf den älteren Ökonomen nicht vorwerfen, dass ihr Begriff des Wachstums sehr allgemein und unpräzise war. Sie standen am Anfang der kapitalistischen Entwicklung, so dass es nicht verwunderlich ist, dass sie auch einiges missverstanden oder ganz falsch verstanden haben. Unter anderem haben sie es für nicht erforderlich gehalten, zwischen dem extensiven Wachstum und der Steigerung der Produktivität zu unterscheiden, was aber am meisten zu bedauern ist, sie haben - mehr oder weniger - beides auf die Akkumulation des Kapitals und das Sparen zurückgeführt. Marx war der erste, der versuchte, diese Auffassung mathematisch zu modellieren und zu simulieren - wie man heute sagen würde - und hat damit den gravierendsten Fehlern und Irrtümern aus den alten Zeiten der Wirtschaftswissenschaft neue Lebenskraft eingehaucht. Trotzdem verdient sein Versuch eine Würdigung.
Seine Entscheidung für ein Kreislaufmodell war methodologisch richtig. Marx hat nie verheimlicht, dass er dieses Modell schon vorgefunden hat, bei Quesnay, den er übrigens für einen der größten Ökonomen aller Zeiten gehalten hat. Quesnay wollte mit dem Modell ein stationäres Gleichgewicht, oder besser gesagt die ewige Harmonie der Wirtschaft („ordre naturel“) nachweisen, Marx wollte mit ihm zeigen, wie die kapitalistische Wirtschaft wachsen kann. Gerade weil sich Marx für das Kreislaufmodell entschieden hat, konnte er ein sozusagen strukturelles bzw. produktionstechnisches Problem entdecken, dass zu Beginn des Wirtschaftswachstums vorkommt.
Bemerkung: Dieses produktionstechnische Problem ist etwas anderes als das bereits erwähnte gleichgewichtstheoretische Problem, auch wenn es zwischen ihnen einen Zusammenhang gibt. Das gleichgewichtstheoretische Problem ist Marx leider völlig entgangen. Dies lässt sich vor allem darauf zurückführen, dass er zwar das Kreislaufmodell von Quesnay auf eine wachsende Wirtschaft angewandt (die „erweiterte Reproduktion“), aber an den analytischen Methoden nie etwas nachgebessert hat.
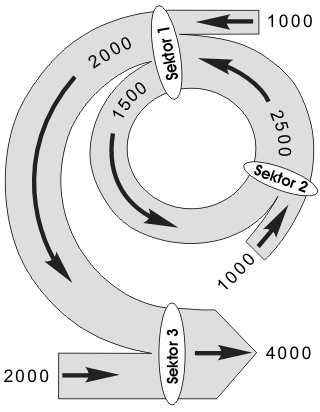
Marx hat bekanntlich sein numerisches Beispiel auf zwei Sektoren reduziert - wie er dies schon bei Quesnay vorfand. Aber in unserem Beispiel mit drei Sektoren lässt sich das produktionstechnische Problem genauso einfach veranschaulichen. Um jetzt nicht „zurückblättern“ zu müssen, stellen wir das Flussdiagram unseres dreisektoralen Modells noch einmal dar.
| |
 |
← Auf das Bild klicken, um es zu vergrößern |
Uns geht es jetzt nicht um gleichgewichtstheoretische Zusammenhänge, so dass wir diese beiseite lassen. Deshalb empfiehlt es sich, dass wir uns für einen Augenblick in die Lage der Ingenieure und Technologen versetzen, die sich um die ganze Wirtschaft kümmern müssen und dabei versuchen, die Frage zu beantworten, wie sie überhaupt wachsen kann. So etwa ging auch Marx in seinen Überlegungen vor. Um wachsen zu können, so seine Folgerung, brauche die Wirtschaft mehr reales Kapital. Aber eine Wirtschaft kann nicht mehr reales Kapital haben als sie gerade besitzt. Der einzige Ausweg heißt dann, laut Marx, das insgesamt verfügbare Kapital der Wirtschaft - also die Produktionsgüter - sektoral anders zu verteilen. Den konsumproduzierenden Unternehmen sollte am Anfang ein bisschen weniger und den Investitionsgüter produzierenden Unternehmen entsprechend mehr von dem bereits verfügbaren Kapital zugeteilt werden. An unserem Beispiel lässt sich dies genauer schildern: Der Sektor 1 sollte dem Sektor 3 weniger und dem Sektor 2 mehr liefern. Die Produktion von Konsumgütern wird sich dann zunächst verringern müssen, aber dem Sektor 2 wird es dadurch möglich werden, seine Produktion zu erweitern. Die größere Menge von Produktionsgütern, welche nun der Sektor 2 daraufhin produzieren wird, bekommt natürlich der Sektor 1, so dass demnächst auch er mehr Produktionsgüter herstellen wird. Und dann wird schließlich auch der Sektor 3 mehr von ihm bekommen können, mehr als es ursprünglich der Fall war, als die Wirtschaft noch nicht angefangen hatte zu wachsen. Stehen nun auch dem Sektor 3 mehr Produktionsgüter zur Verfügung, so ist der Zustand eingetreten, bei dem sich die Produktion aller Sektoren um den gleichen Prozentsatz vergrößert hat. Die Wirtschaft ist gewachsen.
Man muss kein Ingenieur oder Technologe sein, um die geschilderten produktionstechnischen Sachzwänge zu begreifen. Man würde sogar geneigt sein zu meinen, dass dies alles sehr trivial ist und dass es weit überzogen wäre, dies für eine wichtige Entdeckung zu halten. Da muss man aber vorsichtig sein. Ob eine Entdeckung oder eine Erkenntnis von Bedeutung ist oder eben nicht, hängt jedoch wesentlich davon ab, was man vergleicht und womit. Denkt man daran, auf welche tollpatschige - zum teil widersinnige - Weise und in welchem Schneckentempo sich die Wirtschaftswissenschaft seit fast zwei Jahrhunderten entwickelt hat, sollte man jede kleine Entdeckung würdigen. Konkret bedeutet dies, dass man auch die Marxschen Beiträge zur Analyse des Wirtschaftswachstums mit dem vergleichen soll, was die anderen geleistet haben. So betrachtet verdient der Versuch von Marx doch viel Lob. Was haben nämlich später die Neoliberalen (Neoklassiker) mit ihrem Gleichgewichtsmodell zur Wachstumstheorie beigetragen? Nichts. Und schon gar nichts haben die hoch mathematisierten Eingutmodelle gebracht.
An den Fehlern, die Marx begangen hat, gibt es natürlich nichts zu beschönigen. Man kann sie vielleicht nur bedauern: Wer könnte nämlich sagen, wo die ökonomische Theorie heute wäre, hätte Marx nur ein bisschen mehr Sinn für die Mathematik gehabt. Vielleicht hat das Schicksal oder die Vorsehung es so gewollt. Es könnte sein, dass womöglich auch wegen seiner Fehler das kreislauftheoretische Modell durch das partikular-mechanische von Walras und Pareto ersetzt worden ist. Aber wir können da nur rätseln. Der Niedergang der Kreislaufanalyse hatte vermutlich auch damit zu tun, dass Marx in seinem Modell - wie eben erwähnt - nur zwei Sektoren hatte, die entsprechend nur zwei Güterarten produzieren: Konsumgüter und Produktionsgüter. Das war eindeutig zu wenig. Das darauf folgende neoliberale Modell wurde nämlich mathematisch so konstruiert, dass es beliebig viele Güter erfassen kann. Auf den ersten Blick konnte dies als ein riesiger Fortschritt betrachtet werden. Bei genauerem Hinsehen war dies aber eine theoretische Mogelpackung. Das ist am einfachsten zu begreifen, wenn wir uns an die Herkunft des „neuen“ Modells erinnern, nämlich die klassische Mechanik.
In der Mechanik ist ein Apfel identisch mit einer Birne, vorausgesetzt beide wiegen gleich. Man kann folglich in dem mathematischen Modell (Gleichungssystem) des Kräftegleichgewichts alle Birnen mit Äpfeln austauschen und umgekehrt, und genauso beliebig kombinieren, das Ergebnis wird gleich bleiben. Eine solche strukturelle Freiheit gibt es in keinem anderen naturwissenschaftlichen Modell. Diese uneingeschränkte Freiheit hat das neoliberale Modell geerbt und sie zu einer idiotensicheren Freiheit hochstilisiert. Das Modell kann also in der Tat beliebig viele Güter in sich aufnehmen, diese können sich jedoch nicht mehr qualitativ, sondern nur quantitativ voneinander unterscheiden. Damit diese fast unfassbare Simplizität (Unterkomplexität) nicht sofort ins Auge sticht, wurde das Modell mit vielen Schichten einer komplizierten (und nutzlosen) Mathematik überdeckt.
Genauer genommen, gibt es also in der neoliberalen Theorie des allgemeinen Gleichgewichts, aus der auch das Wachstum erklärt wird, nur ein einziges universelles Gut, das in verschiedenen Anteilen verstreut wird. Als solches ist dieses Gut zugleich auch unendlich flexibel. Hier kann man sich noch einmal an Schumpeter erinnern, der im neoliberalen Modell den Stein der Weisen sieht, aber trotzdem beunruhigt ist und Bedenken äußert, dass nach der Logik dieses Modells „eine Maschine nach dem Willen ihres Besitzers unmittelbar in einen Lehnstuhl überführt werden kann“ und umgekehrt. Schließlich kann in diesem Modell auch das von Marx erkannte strukturelle Problem gar nicht auftauchen. Das Investieren bedeutet in diesem Modell nur, dass man die vorhandene Gütermenge anders aufteilt: es werden etwas mehr Güter der Wirtschaft (Investoren) zur Verfügung gestellt und entsprechend weniger den Konsumenten (Sparern). Wie viel es konkret sein wird, bestimmt das Zinsniveau. Nachdem sich auf diese Weise die Güterproduktion vergrößert hat, kann sich alles wiederholen, und zwar beliebig lange. So einfach ist die neoliberale Welt, dass es eine einfachere gar nicht geben kann.
Schon diese kurze Erörterung zeigt, warum Marx trotz der Fehler mehr über die ökonomische Entwicklung sagen konnte als die auf dem neoliberalen partikel-mechanischen Modell begründete „bürgerliche“ Theorie. Dieses neoliberale Modell vereinfacht bzw. reduziert das Phänomen Wirtschaft auf nur einige weinige Eigenschaften: Es ist eine Reduktion der Komplexität fast auf Null. Und wenn ein Modell dermaßen einfach und inhaltsleer ist, was kann in ihm schon schief laufen. Es kennt schließlich auch keine Probleme beim Wirtschaftswachstum: weder produktionstechnische noch gleichgewichtstheoretische. Folglich kann man in der Wirtschaft alles der Freiheit überlassen. Auf so einen Schwachsinn muss man erst kommen. Würde es der Menschheit gelingen, sich aus der mörderischen Umarmung der neoliberalen Theorie zu befreien, werden die zukünftigen Generationen große Mühe haben zu begreifen, wie eine dermaßen idiotische Theorie so lange die Köpfe der Menschen, die nicht alle beim Kapital geistig prostituierte Opportunisten waren, beherrschen konnte.
Das allgemeine Gleichgewicht beim extensiven Wirtschaftswachstum
Das Kreislaufmodell ist also die richtige - ich glaube sogar die einzig richtige - analytische Grundlage für die Untersuchung des Wachstums, weil sich mit ihm die produktionstechnischen Probleme des Wachstums analytisch genau berücksichtigen und nachvollziehen lassen. Auf dieser Grundlage lässt sich folglich auch der Übergang zum Wachstum gleichgewichtstheoretisch erfassen, aber diese schwierige Problematik verschieben wir auch jetzt noch nach vorne. Wie bereits angedeutet, können wir sie überspringen - was fast buchstäblich zu verstehen wäre -, indem wir an die bereits durchgeführte Untersuchung des Produktivitätswachstum anknüpfen.
Bei dieser Untersuchung haben wir angenommen, dass der Sektor 2 eine neue Produktionsmethode erfunden hat, mit der er bei gleicher Produktion (Output) ein Drittel der Produktionsgüter sparen kann. Als er diese Methode verwendet hat, stand der Wirtschaft auf einmal Kapital im Wert von 500 frei zur Verfügung. Damals haben wir uns entschieden, dass diesen Überschuss gänzlich der Sektor 3 übernimmt. Damit haben wir gesorgt, dass alle Auswirkungen der Innovation alleine dem Produktivitätswachstum zuzuschreiben sind. Wenn wir jetzt einen Teil des freigewordenen Kapitals auch dem Sektor 2 zur Verfügung stellen, lässt sich alles, was dann im System zusätzlich passiert, dem extensiven Wachstum zuschreiben. Damit ist im Groben umrissen, wie wir das Wachstum mit unserem numerischen Beispiel erforschen wollen; jetzt führen wir diese Aufgabe Schritt für Schritt durch.
Bei unserer Untersuchung des Produktivitätswachstums wurden alle Vorbereitungen für den Technologiewechsel im Sektor 2 in der Reproduktionsperiode t+1 durchgeführt. Diesmal soll die Wirtschaft in dieser Reproduktionsperiode zugleich auch für ihr extensives Wachstum bereitgemacht werden. Wie bereits erwähnt, deshalb überlassen wir dem Sektor 3 nicht mehr die ganze Menge des freigewordenen Kapitals, sondern nur im Wert von 400. Den Rest von 100 behält der Sektor 2, damit er seine Produktion um 10% vergrößern kann. Uns interessieren die Transaktionen die dabei vonstatten gehen, die sich mit Hilfe der Tauschtabelle verdeutlichen und verstehen lassen. Wir haben diese Tabelle schon bei früheren Untersuchungen benutzt und dabei die Handhabung genauer geklärt, deshalb können wir hier schneller vorangehen.
wurden alle Vorbereitungen für den Technologiewechsel im Sektor 2 in der Reproduktionsperiode t+1 durchgeführt. Diesmal soll die Wirtschaft in dieser Reproduktionsperiode zugleich auch für ihr extensives Wachstum bereitgemacht werden. Wie bereits erwähnt, deshalb überlassen wir dem Sektor 3 nicht mehr die ganze Menge des freigewordenen Kapitals, sondern nur im Wert von 400. Den Rest von 100 behält der Sektor 2, damit er seine Produktion um 10% vergrößern kann. Uns interessieren die Transaktionen die dabei vonstatten gehen, die sich mit Hilfe der Tauschtabelle verdeutlichen und verstehen lassen. Wir haben diese Tabelle schon bei früheren Untersuchungen benutzt und dabei die Handhabung genauer geklärt, deshalb können wir hier schneller vorangehen.
Zuerst erstellen wir nur den oberen Teil dieser Tabelle. Wie damals, nachdem wir die bereits bekannten Werte eingetragen haben, bleiben noch mehrere Felder leer, die sich aber berechnen lassen.
Wenn alle Sektoren ihr Einkommen ausgeben, lässt sich Spalte 6 nur auf eine Weise ausfüllen. Weil diese Spalte identisch mit Zeile 3 ist, haben wir damit zugleich auch die Werte für sie herausgefunden. Wenn man Zeile 4, in der Nettoeinkünfte stehen, von der Zeile 3 - in der von dem betreffenden Sektor gekaufte Konsumgüter stehen - subtrahiert, bekommt man die Ersparnisse bzw. Investitionen des betreffenden Sektors. Nun ist unsere Tauschtabelle komplett.
Wir stellen fest, dass die Summe der Ersparnisse bzw. Investitionen der Wirtschaft gleich Null ist. Weil der Wert der Produktionsgüter in der Reproduktionsperiode t+1 gleich wie in der Reproduktionsperiode t ist, ist die Differenz zwischen ihnen ebenfalls gleich Null. Die allgemeine Gleichung des Sparens gilt also: YK′ = I′ = S′ . Uns interessiert aber, ob diese Gleichung auch dann gültig bleibt, wenn das Wachstum begonnen hat. Dies geschieht schon in der nächsten Reproduktionsperiode, indem der Sektor 2 seine Produktion vergrößert.
Um die dynamische Analyse nicht unnötig zu verkomplizieren, lassen wir die Einzelpreise aller Güter unverändert. Damit auch die Einzelpreise des Sektors 2 gleich bleiben, muss dem Sektor der Profit aus Einsparungen bzw. Innovationen (Q) überlassen werden. Nachdem der Sektor seine Produktion um 10% erhöht hat, wird auch dieser Profit gleichermaßen steigen. Dies und alles andere, was in der nächsten Reproduktionsperiode geschieht, zeigen die folgenden zwei Tabellen.
| |
| t +2 |
Produktionsprozess |
| |
| Sektor 1: |
| Sektor 2: |
| Sektor 3: |
|
| |
K |
|
Ÿ |
|
Q |
|
Y |
|
| |
2500.00 |
+ |
1000 |
|
|
= |
3500.00 |
|
| |
1000.00+100 |
+ |
1000+100 |
+ |
500+50 |
= |
2750.00 |
|
| |
2000.00+400 |
+ |
2000+400 |
|
|
= |
4800.00 |
|
|
|
|
| Kapitalbeschaffung |
| für Reproduktionsperiode t +3 |
|
| |
|
K1t+3 |
|
= |
|
2750.00 |
|
|
|
|
| |
|
K2t+3 |
|
= |
|
1100.00 |
|
|
|
|
| |
|
K3t+3 |
|
= |
|
2400.00 |
|
|
|
|
|
|
|
Weil der Sektoren 2 seine Produktion vergrößert hat, hat sich die Produktion der Sektoren, welche die Produktionsgüter herstellen, während dieser Reproduktionsperiode zusammen genommen um 250 vergrößert (YK′). Wenn wir jetzt die Tauschtabelle entwerfen
stellen wir fest, dass auch die Investitionen und Ersparnisse den Wert 250 haben. Die allgemeine Gleichung des Sparens ( YK′ = I′ = S′ ) hat sich also weiterhin als gültig erweisen.
Wir schauen uns noch an, was in der Reproduktionsperiode t+3 geschieht. Diesmal wird auch der Sektor 1 seine Produktion vergrößern. Die Einzelpreise aller Güter lassen wir auch weiterhin unverändert.
| |
| t +3 |
Produktionsprozess |
| |
| Sektor 1: |
| Sektor 2: |
| Sektor 3: |
|
| |
K |
|
Ÿ |
|
Q |
|
Y |
|
| |
2750.00 |
+ |
1000+100 |
|
|
= |
3850.00 |
|
| |
1100.00 |
+ |
1100 |
+ |
550 |
= |
2750.00 |
|
| |
2400.00 |
+ |
2400 |
|
|
= |
4800.00 |
|
|
|
|
| Kapitalbeschaffung |
| für Reproduktionsperiode t +4 |
|
| |
|
K1t+4 |
|
= |
|
2750.00 |
|
|
|
|
| |
|
K2t+4 |
|
= |
|
1100.00 |
|
|
|
|
| |
|
K3t+4 |
|
= |
|
2750.00 |
|
|
|
|
|
|
|
Nachdem auch der Sektor 1 seine Produktion vergrößert hat, ist der Wert der Produktionsgüter in dieser Reproduktionsperiode zusammengenommen um 350 gestiegen (YK′). Wenn wir jetzt für die Werte der obigen zwei Tabellen in die Tauschtabelle einfügen und diese vervollständigen,
stellen wir fest, dass die Investitionen und Ersparnisse ebenfalls 350 betragen. Auch diesmal gilt also die allgemeine Gleichung des Sparens. Dem Leser ist es überlassen zu prüfen, dass die Wirtschaft schon in der nächsten Reproduktionsperiode im stationären Zustand wäre. Wir konnten also feststellen und es damit als nachgewiesen betrachten, dass die allgemeine Gleichung des Sparens ihre Gültigkeit behält, auch wenn die Wirtschaft extensiv wächst: quod erat demonstrandum.
Wenn wir uns den Kapitalstock in dem neuen stationären Zustand anschauen, stellen wir fest, dass er um 600 gewachsen ist, nämlich von (25001 + 15002+ 20003)t auf (27501 + 11002 + 27503)t+4. Dieser Kapitalzuwachs entspricht genau der Summe der Ersparnisse in dieser Zeit (250t+3 + 350t+4), was uns auf eine indirekte Weise bestätigt, dass wir richtig gerechnet haben. Alle Ersparnisse der Sparer sind also mit dem neu geschaffenen realen Kapital gedeckt - zumindest solange die Börsen und Banken mit diesen Ersparnissen nicht geschachert haben. Das Verhältnis zwischen den Ersparnissen und dem Konsum ist dagegen viel komplizierter, was wir uns jetzt genauer anschauen wollen.
Das nominale und das reale Sparen beim extensiven Wirtschaftswachstum
Schon aus unserem sehr einfachen Beispiel mit den Weizen produzierenden Bauern, mit dem wir diesen thematischen Bereich begonnen haben, ließ sich erahnen, dass das reale und nominale Sparen ziemlich unterschiedliche Größen sein können. Wir haben schon damals folgende Unterschiede in Betracht gezogen:
- Das nominale Sparen muss nicht bedeuten, dass real weniger Güter konsumiert werden.
- Man kann den Konsum steigern, ohne dass man zuerst für eine bestimmte Zeit auf den Konsum verzichtet.
- Das nominale Sparen sagt nichts über die Änderungen im realen Kapitalstock (Kapitalakkumulation) aus.
- Den nominalen Ersparnissen muss keine produktive Leistung innewohnen.
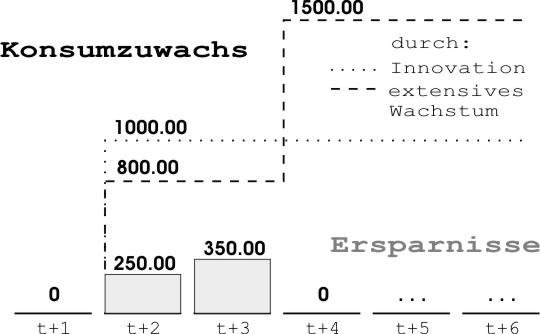
Als wir dann das Gleichgewicht der Wirtschaft genauer untersucht haben - bei den Preisänderungen und dem Produktivitätswachstum -, hat sich herausgestellt, dass fast oder sogar alle diese Unterschiede zur Geltung kamen. Die mikroökonomische oder nominale Welt und die makroökonomische oder reale Welt sind völlig auseinander gedriftet. Bei dem extensiven Wachstum lässt sich etwas anderes feststellen. Hier kommen sich das reale und nominale Sparen sehr nahe. Da uns die Zahlen dafür zur Verfügung stehen, lässt sich dies schnell quantitativ genau prüfen bzw. nachweisen. Diese Zahlen stehen im nächsten Bild. Im Bild sind auch die Ergebnisse des bereits untersuchten Produktivitätswachstums eingetragen, damit wir zugleich auch vergleichen können.
| |
 |
|
Die gepunktete Linie zeigt, um wie viel sich die Konsumproduktion vergrößert hat, als der Sektor 2 eine neue Produktionsmethode eingeführt hat, ohne dabei seine Produktion zu vergrößern. In diesem Fall gab es kein Sparen - wenn man die Wirtschaft als ein Ganzes (makroökonomisch) betrachtet -, so dass es auf dem Bild auch nicht vorkommt. Als wir dann den Sektor 2 auch noch (extensiv) wachsen ließen, stellte sich heraus, dass es zwei Reproduktionsperioden lang positive (makroökonomische) Ersparnissummen gab, bis die Wirtschaft ihr Wachstum abgeschlossen und den neuen stationären Zustand erreicht hat. Diese Ersparnisse sind als zwei Balken dargestellt. Die gestrichelte Linie zeigt, wie sich die Konsumproduktion entwickelt, wenn die Wirtschaft extensiv gewachsen ist.
Bemerkung: Hätten wir uns für einen stärkeren Wachstumssprung entschieden als 10%, dann wären diese Balken größer, und umgekehrt. Die Konsumgüterproduktion würde bei einem stärkeren Wachstumsschub zuerst weniger, aber später desto stärker anwachsen und umgekehrt. Man kann hier noch beiläufig erwähnen, dass der Sektor 2 nicht nur in der Reproduktionsperiode t+2 seine Produktion erweitern konnte, sondern auch bei allen weiteren Reproduktionsperioden - theoretisch sogar unendlich lange. Bei jeder weiteren „Aufstockung“ des Kapitals (Investitionen) im Sektor 2 würde sich auch die Zahl der Übergangsperioden, bei denen gespart werden müsste, vergrößern. Das alles werden wir uns aber erst bei der Analyse der ökonomischen Zyklen näher anschauen. |
|
Wenn wir vergleichen, stellen wir fest, dass in dem Fall, als die Wirtschaft auch extensiv wuchs, die Menge der produzierten Konsumgüter in den Reproduktionsperioden 2 und 3 um 200 kleiner ist. Die Wirtschaft musste also zwei Reproduktionsperioden lang auf je 200 verzichten (abstinieren), was sich aber sehr gelohnt hat. Schon in Reproduktionsperiode 4 und allen darauf folgenden ist die produzierte Konsummenge um 500 größer geworden, als wenn die Wirtschaft nicht gespart bzw. investiert hätte. Wenn man sich das bewusst macht, kann man gut verstehen, warum Adam Smith das Sparen immer mit Lob überschüttet hat:
„Sparsamkeit und nicht Erwerbfleiß ist die unmittelbare Ursache für Anwachsen des Kapitalbestandes. ... Ohne Ersparnis kann der Kapitalbestand niemals größer werden. Die Sparsamkeit erhöht die zum Unterhalt produktiver Leute bestimmten Fonds, wodurch sie die Zahl derer vergrößert, deren Arbeit den Gütern einen Mehrwert verleiht.“

Es lässt sich nicht daran zweifeln, dass die kapitalistische Wirtschaft am Anfang ihrer historischen Entwicklung, in der Zeit also, die Smith noch erlebte und über die er schrieb, viel Kapital brauchte, und folglich war es auch nicht ganz falsch, viel zu sparen. Wenn die Wirtschaft extensiv wächst, können die Menschen in der Tat getrost das tun, was sie sonst so gerne tun, nämlich sparen, ohne dass damit das Gleichgewicht gestört wird.
| |
 |
Die empirischen Daten sagen uns, dass der Kapitalstock in den westlichen kapitalistischen Wirtschaften noch mehrere Jahrzehnte nach Marx Tod wuchs, bis zur Großen Depression, danach jedoch nicht mehr. Seitdem entspricht die Kapitalmenge, über welche die entwickelten kapitalistischen Nationen verfügen, etwa dem Gegenwert von vier Jahresproduktionen. Wir können also davon ausgehen, dass seitdem das Produktivitätswachstum kaum etwas mit dem realen Sparen zu tun hat. Die Ausnahmen sind Naturkatastrophen und vor allem Kriege. Die alten Beobachtungen, dass nach Kriegen „Wirtschaftswunder“ kommen, lassen sich also gleichgewichtstheoretisch vollständig erklären. Diese Erklärung ist eine andere, als die weit verbreitete, dass angeblich der Mangel an den Konsumgütern, der nach den Kriegen immer herrscht, die ökonomische Aktivität belebt. Wäre dem so, dann ließe sich nicht beantworten, warum die Depressionen oft so lange dauern und nach den Kriegen alles so schnell voran geht. Die Depressionen sind nämlich ebenfalls starke Produktionseinbrüche, die ganz bestimmt nicht deshalb hingenommen werden, weil die Menschen es satt haben zu konsumieren. Der angebliche Bedarf an Konsumgütern nach den Kriegen erklärt also gar nichts. Die Volkswirtschaften wachsen nicht einfach deshalb, weil sich die Menschen ein besseres Leben wünschen - weil sie gern mehr konsumieren wollen. Nicht die fehlenden Konsumgüter erklären also den Wirtschaftsboom nach den Kriegen, sondern das fehlende Kapital bzw. die fehlenden Produktionsgüter, die erst produziert werden müssen. Und indem man gerade diese Güter produziert - indem also die Wirtschaft (auch) extensiv wächst -, können die Menschen auch das tun, was sie sonst tun wollen, nämlich sparen.
Heben wir noch abschließend hervor, dass die oben ausgerechneten und in dem Bild dargestellten Ersparnisse nur für den Fall gelten, wenn die Einzelpreise konstant bleiben. Bei fallenden Preisen (der Produktionsgüter) würden sich auch die Sparsummen verringern, so dass das Sparen wieder ein Gleichgewichtsproblem verursachen kann. Aber darüber später.
|
|
|
| |
|
|
|
|