Der periodische Absturz der freien Wirtschaft nach der Hochkonjunktur kommt unerwartet und verläuft schnell. Dann folgt eine längere Zeit, in der die Wirtschaft Probleme hat wieder auf den Wachstumskurs zu gelangen, die man als Krise oder Depression bezeichnet. Sie ist eine der vier Phasen des Konjunkturzyklus. Keynes hat den Zustand der Wirtschaft während der Depression als Gleichgewicht bei Unterbeschäftigung bezeichnet. Von einem Gleichgewicht zu sprechen hat deshalb eine gewisse Berechtigung, weil die Depression ein gewissermaßen stabiler Zustand ist, jedoch auf einem niedrigen Niveau. Es gibt aber auch einen gute Grund, diesen Zustand doch nicht als Gleichgewicht, sondern als Ungleichgewicht zu betrachten. Wie wir jetzt sehen werden, versucht die Wirtschaft in diesem Zustand zu wachsen, aber eine längere Zeit scheitern all ihre Versuche. Die vergeblichen Mühen der Unternehmen zu investieren, kann man mit dem Unterfangen von Sisyphos vergleichen, dem ganz kurz vor dem Gipfel der Stein entgleitet und den Berg herunter rollt, so dass er immer wieder von vorne beginnen muss. Und dies obwohl Sisyphos nichts falsch macht. Auch die Unternehmer machen nichts falsch, sie tun während der Depression genau dasselbe, was sie auch während der Hochkonjunktur tun, sie investieren wie gewohnt, die Investitionen misslingen aber immer wieder. Das ist der wahre Grund, warum die Depression so zäh ist und manchmal so lange dauert. Sollte man sie überhaupt als einen stabilen Zustand verstehen, dann als einen des permanenten Scheiterns. Deshalb werden wir diesen Zustand weiterhin als Ungleichgewicht bezeichnen.
Wir werden jetzt mit der nötigen analytischen Präzision und Stringenz nachweisen, dass sich das Scheitern der Investitionen während der Depression mit dem Nachfragemangel erklären lässt. Der Nachfragemangel ist natürlich kein neuer Ansatz in der ökonomischen Theorie. Die unglücklichen Pioniere dieses Ansatzes am Anfang des 19. Jahrhunderts waren bekanntlich Sismondi und Malthus. Sie konnten damals mit ihren Argumenten und Analysen nicht überzeugen. Erst Keynes, ein Jahrhundert später, ist es gelungen, den Durchbruch für die Nachfragetheorie zu schaffen. Er führte aber den Nachfragemangel auf Geldprobleme bzw. auf das Geldhorten zurück, weshalb wir auch von einer monetären Nachfragetheorie sprechen können. Diese Vereinfachung und Reduzierung des Nachfrageproblems auf Geldhorten - wie bereits erörtert - hatte zur Folge, dass von der monetären Nachfragetheorie nur eine Stagnationstheorie übrig geblieben ist. Sie kann gerade noch die Depression deuten, mit dem Absturz der Wirtschaft hat sie schon große Probleme. Wie es zum Aufschwung kommt und warum die Marktwirtschaft für eine geraume Zeit gut funktionieren kann, das kann sie gar nicht erklären.
Um jetzt nicht einen falschen Eindruck zu vermitteln, heben wir ausdrücklich hervor, dass die monetäre Nachfragetheorie trotzdem ein großer Erfolg war, nicht nur ein praktischer, sondern auch ein theoretischer. Nur ihr Geltungsbereich hat sich als zu schmal erwiesen. Sie ist unterkomplex und als solche ist sie nicht allgemein, wie es sich Keynes erhofft hat, sondern nur speziell. Ihr ist es schließlich nicht gelungen, die Funktionsweise der Wirtschaft im Allgemeinen zu erklären. Ihre Verdienste sind vor allem darin zu sehen, dass sie überhaupt herausgefunden hat, dass es so etwas wie das Verschwinden des Geldes - wegen der Geldhortung der Banknoten oder auf andere Weise - überhaupt gibt. Dies lässt sich aber nicht als die primäre Ursache und Quelle der ökonomischen Probleme der Marktwirtschaft verstehen. Folglich kann man das Geld nicht als den Anfang allen Übels betrachten. Deshalb müssen wir die Nachfragetheorie auf eine andere Grundlage stellen.
Der Nachfragemangel wird bei uns bedeuten, dass das Einkommen der Wirtschaft nicht immer ausreicht, alle bereits hergestellten bzw. angebotenen Güter zu kaufen. Während der Depression entsteht dieser Mangel an der Nachfrage bzw. am Einkommen dann, (1) wenn die Unternehmen zu sparen und zu investieren versuchen und (2) wenn die Preise fallen. Beides hat mit dem Geld, also mit dem Verschwinden des Geldes - in welcher Form auch immer -, nichts (direkt) zu tun. Um ganz deutlich zu machen, dass das fehlende Einkommen in keinem festen Zusammenhang mit dem Geld steht, werden wir in unserer Analyse der ökonomischen Zyklen das Geld gar nicht berücksichtigen.
Verba docent, exempla trahunt - Worte lehren, Beispiele reißen mit, sagt schon ein lateinisches Sprichwort. In diesem Beispiel produzieren zwei Sektoren Produktionsgüter und der dritte Konsumgüter. Zum besseren Verständnis können wir uns die drei Sektoren als konkrete Produktionsbereiche vorstellen. Dann soll der Sektor 2 Rohstoffe und Halbfabrikate, der Sektor 1 Maschinen und Anlagen und der Sektor 3 Konsumgüter herstellen. Das folgende Flussdiagramm zeigt diese dreisektorale Wirtschaft in einem Zustand, der sich beliebig lange unverändert wiederholen lässt. Deshalb wird er als stationär bezeichnet.
| |
| Nettoeinkommen |
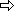 |
| (Wertschöpfung) |
|
|
|
 |
 |
Nettoeinkommen |
| (Wertschöpfung) |
| |
|
 |
Nettoeinkommen |
| (Wertschöpfung) |
|
| Nettoeinkommen: |
| Sektor 1: |
1000 |
| Sektor 2: |
1000 |
| Sektor 3: |
2000 |
|
|
|
4000 |
|
| |
| Konsumproduktion: |
| Sektor 1: |
0 |
| Sektor 2: |
0 |
| Sektor 3: |
4000 |
|
|
|
4000 |
|
|
Die externen Inputs der Sektoren beinhalten verschiedene Leistungen bzw. dafür ausbezahlte Einkünfte (Löhne, Sondervergütungen, Profite, Dividenden, Grundrente, Zinsen, ...), die in der Wirtschaft einerseits als Kosten und andererseits als Nettoeinkünfte fungieren. Das Flussdiagramm ist eigentlich die grafische Darstellung des stationären Zustandes, den wir als numerisches Beispiel schon mehrmals benutzt haben. In einem solchen Zustand sind alle Güterströme - gemessen in absoluten Preisen - geschlossen. Das betrifft jeden einzelnen Sektor, aber den Konsummarkt genauso: Die gesamte Nachfrage nach den Konsumgütern (die Summe der externen Inputs aller Sektoren) ist nämlich gleich dem gesamten Angebot an Konsumgütern (dem Output des Sektors 3). Das wird in der Tabelle dargestellt.
Heben wir nur noch ausdrücklich hervor, dass wir in unserer Analyse der Depression die realen Disproportionalitäten - heute sagt man dazu strukturelle Probleme - nicht berücksichtigen, und das wollen wir auch weiterhin nicht tun. Natürlich trifft es zu, dass es in der Wirtschaft (reale) Disproportionalitäten immer gibt, und zwar mehr als genug, aber sie gehören nicht zu unserer Erklärung der ökonomischen Zyklen. Bei uns ist nicht die Summe der vielen kleinen falschen Entscheidungen oder irrationalen Fehltritte von Einzelnen die Ursache des periodischen Absturzes der Markwirtschaft.
Wenn man nicht die infinitesimale Mathematik bemühen will - die sich übrigens in der Wirtschaftswissenschaft nicht als sehr nützlich erwiesen hat - teilt man den Wirtschaftsablauf auf (diskrete) Reproduktionsperioden auf. So hat es schon Quesnay getan. Damit macht man die Analyse nicht nur realistischer, sondern zugleich verschafft man sich auch eine bessere Möglichkeit, die Wirtschaftsaktivitäten quantitativ zu untersuchen. Wir können etwa annehmen, dass eine Reproduktionsperiode ein Jahr dauert - eine andere zeitliche Einheit wäre aber genauso gut. Um es zu verallgemeinern, soll der stationäre Zustand als die Reproduktionsperiode t bezeichnet werden.
Weil es keine Disproportionalitäten gibt und alle Sektoren ihre ganze Produktion absetzen, ist die Summe der Kosten bei jedem Sektor notwendigerweise gleich dem Preis der von ihm hergestellten Güter. Diese Identität bedeutet nichts anderes als das, was vom Sayschen Gesetze behauptet wird, und so betrachtet lässt sich diesem Gesetz gar nichts vorwerfen. Auch die Summe aller Nettoeinkünfte (1000+1000+2000) ist gleich dem Wert der vom Sektor 3 produzierten Konsumgüter (4000), so dass makroökonomisch die ganze Wirtschaft ebenfalls im Gleichgewicht ist. Wir haben das gleiche Beispiel schon mehrmals benutzt und dazu schon einiges gesagt. Trotzdem gehen wir es jetzt noch einmal durch, damit der Leser nicht auf die älteren Beiträge zurückzugreifen braucht. Wir fangen mit zwei Tabellen an, die genauer zeigen, was in der Wirtschaft vor sich gehen würde, wenn sich auch in der nächsten Reproduktionsperiode t+1 in der Wirtschaft nichts ändern würde - wenn die Wirtschaft gar nicht anfangen wollte zu wachsen.
| |
| t + 1 |
Produktionsprozess |
| |
| Sektor 1: |
| Sektor 2: |
| Sektor 3: |
|
| |
K |
|
Ÿ |
|
|
|
Y |
|
| |
2500.00 |
+ |
1000 |
|
= |
|
3500.00 |
|
| |
1500.00 |
+ |
1000 |
|
= |
|
2500.00 |
|
| |
2000.00 |
+ |
2000 |
|
= |
|
4000.00 |
|
|
|
|
| Kapitalbeschaffung |
| für Reproduktionsperiode t + 2 |
|
| |
K1t+2 |
= |
K1t+1 |
|
= |
|
2500.00 |
|
| |
K2t+2 |
= |
K2t+1 |
|
= |
|
1500.00 |
|
| |
K3t+2 |
= |
K3t+1 |
|
= |
|
2000.00 |
|
|
|
Die linke Tabelle beschreibt den Produktionsprozess aller Sektoren einzeln. Die Sektoren 1 und 2 stellen Güter her, welche die Wirtschaft nicht verlassen, vereinfacht gesagt: Kapitalgüter. Wenn diese Güter fertig gestellt sind, werden sie an die Sektoren distribuiert, wie es die rechte Tabelle darstellt. Hätten die Sektoren 2 und 3 am Ende der Reproduktionsperiode t+1 ihre Produktion tatsächlich so distribuiert, wie es die Tabelle rechts zeigt, dann würden alle drei Sektoren in der nächsten Reproduktionsperiode t+2 gleiche Mengen von Gütern herstellen wie zuvor. Alles würde sich genauso wiederholen wie in allen vorigen Reproduktionsperioden. Das wollen wir aber nicht, sondern wir wollen diesen stationären Zustand verlassen.
Die einzige Möglichkeit, die Wirtschaft auf den Wachstumspfad zu bringen, besteht darin, zuerst Sektor 2 zu ermöglichen, seine Produktion zu steigern, auch wenn Sektor 3, der Konsumgüterhersteller, deswegen gezwungen wird, seine Produktion zu drosseln. Man spricht in diesem Zusammenhang von Reallokation der Produktionsmittel (des Kapitals). Die produktionstechnischen Gründe für die Reallokation ergeben sich schon unmittelbar aus dem Flussdiagramm. Nur wenn Sektor 2 zuerst seine Produktion steigert, wird später auch Sektor 1 mehr investieren und in einem weiteren Schritt auch mehr Produktionsgüter herstellen können, die schließlich - zum Teil - auch dem Sektor 3 zugute kommen werden, so dass es schließlich allen Sektoren der Wirtschaft möglich sein wird zu wachsen. Wenn wir den Übergang zum Wachstum - mit der Reallokation an Ende der Reproduktionsperiode t+1 - wieder mit zwei Tabellen darstellen, wird sich nur die rechte Tabelle ändern, und zwar wie dargestellt:
| |
| t + 1 |
Produktionsprozess |
| |
| Sektor 1: |
| Sektor 2: |
| Sektor 3: |
|
| |
K |
|
Ÿ |
|
|
|
Y |
|
| |
2500.00 |
+ |
1000 |
|
= |
|
3500.00 |
|
| |
1500.00 |
+ |
1000 |
|
= |
|
2500.00 |
|
| |
2000.00 |
+ |
2000 |
|
= |
|
4000.00 |
|
|
|
|
| Kapitalbeschaffung |
| für Reproduktionsperiode t + 2 |
|
| |
K1t+2 |
= |
K1t+1 |
|
= |
|
2500.00 |
|
| |
K2t+2 |
= |
K2t+1 + 120 |
|
= |
|
1620.00 |
|
| |
K3t+2 |
= |
K3t+1 - 120 |
|
= |
|
1880.00 |
|
|
|
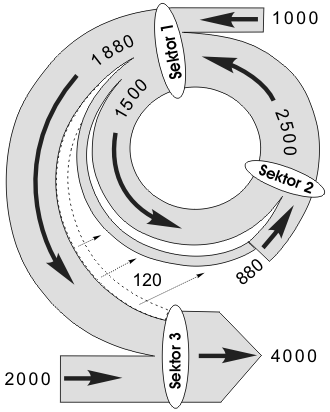
Durch die Entscheidung des Sektors 2 zu investieren, hat sich aber noch einiges mehr im System geändert. Wir stellen diesen Zustand, in dem die Wirtschaft zu wachsen beginnt, mit einem Flussdiagram dar.
| |
 |
|
| Nettoeinkommen: |
| Sektor 1: |
1000 |
| Sektor 2: |
880 |
| Sektor 3: |
2000 |
|
|
|
3880 |
|
| |
| Konsumproduktion: |
| Sektor 1: |
0 |
| Sektor 2: |
0 |
| Sektor 3: |
4000 |
|
|
|
4000 |
|
|
Unser numerisches Beispiel ist dermaßen einfach, dass sich schon im Kopf errechnen lässt, dass jetzt der Konsummarkt, also Sektor 3, Probleme hat seine bereits hergestellten Güter abzusetzen. Es gibt aber manches, was sich aus dem Flussdiagram und den letzten zwei Tabellen nicht unmittelbar entnehmen lässt. Da kann uns eine weitere Tabelle, welche die Transaktionen jedes Sektors numerisch erfasst, helfen. Wir haben auch eine solche Tauschtabelle schon benutzt. Sie macht es möglich, dass wir auf mathematische Gleichungen verzichten, zumindest wie in unserem Fall, wenn die Datenmenge klein ist. Für die Leser, welche die vorigen Beiträge mit solchen Tabellen nicht gelesen haben, zeigen wir jetzt Schritt für Schritt, wie sie entworfen wird, und zwar für unseren konkreten Fall. Wir fangen mit dem Entwurf des oberen Teils dieser Tauschtabelle an. Die Werte, die wir für sie benötigen, können wir aus den vorigen zwei Tabellen entnehmen, aber das Flussdiagramm gibt sie auch her.
Die linke Hälfte der Tabelle zeigt, wie viel die (zwei) Sektoren, die die Produktionsgüter herstellen, verkaufen, und an wen sie verkaufen; die rechte Hälfte zeigt von wem alle Sektoren ihre Produktionsgüter kaufen und wie viel. Wir gehen jetzt davon aus, dass jeder Sektor alles, was von seinen Gesamteinnahmen übrig geblieben ist, nachdem er sich mit den Produktionsgütern versorgt hat, für Konsumgüter ausgibt. Das bedeutet, dass die Linke Seite jeder Zeile gleich wie die rechte sein muss. Das ist mit dem Gleichheitszeichen in der Mitte verdeutlicht. Wir gehen davon aus, dass dann auch die ganze Wirtschaft weiterhin auf allen ihren Ebenen im Gleichgewicht bleiben wird. Sollte sich dies bestätigen, dann wollen wir herausfinden, unter welchen Umständen dies der Fall sein wird.
Wenn wir uns an die Annahme halten, dass alles, was nicht investiert worden ist, konsumierte werden soll, lassen sich die unbekannten Werte für die Felder, wo jetzt Fragezeichen stehen, eindeutig bestimmen. Wenn die Sektoren 1 und 2 ihre restlichen Einkünfte vollständig und unverzüglich für den Kauf der Konsumgüter des Sektors 3 ausgeben, gibt es nur je einen in Frage kommenden Wert für die obigen zwei Felder in der Spalte 6, und zwar 1000 bzw. 880. Diese Spalte stellt das Angebot des gesamten Sektors 3 dar, woraus folgt: Was die Sektoren 1 und 2 von der gesamten Produktion (4000) nicht gekauft haben, muss der Sektor 3 - der Konsumgüterhersteller - selbst verbrauchen. Daraus ergibt sich der Wert 2120 für das unterste Feld der Spalte 6.
Jetzt brauchen wir nur noch die linke Hälfte der Zeile 3 zu bestimmen. Nach einer einfachen Überlegung stellen wir fest, dass die Spalte 6 mit der linken Hälfte der Zeile 3 identisch ist, so dass uns auch alle Felder dieser Zeile bekannt sind. Nun können wir unsere Tauschtabelle vervollständigen und die restlichen Werte ausrechnen.
Die Werte der Zeile 3 zeigen uns, wie viel jeder einzelne Sektor konsumiert hat. In der Zeile 4 stehen die gesamten Nettoeinkünfte des jeweiligen Sektors. Subtrahieren wir die Werte dieser Zeile von den Werten der Zeile 3, haben wir herausgefunden, wie viel die Sektoren aus ihren Nettoeinkünften erspart bzw. investiert haben. Damit ist unsere Tauschtabelle komplett. Das gesamte Ergebnis können wir wie folgt zusammenfassen:
Nachdem der Sektor 2 von seinem Einkommen gespart hat (120), auch wenn er das Gesparte unverzüglich investierte, ist eine gleich große Nachfragelücke (-120) bei den Konsumgütern entstanden. Die übriggebliebenen Nettoeinkünfte aller Sektoren zusammengenommen reichen jetzt nicht mehr aus, alle Konsumgüter nachzufragen. Dies lässt sich übrigens schon aus dem Flussdiagramm unmittelbar entnehmen. Sollten die „überflüssigen“ Konsumgüter nicht auf irgendeine Weise doch vom Markt geräumt werden, dann würde das gerade begonnene Wachstum, also das Investieren beim Sektor 2, volkswirtschaftlich zwecklos. Wegen der Absatzprobleme wird nämlich der Sektor 3 sogar weniger Kapitalgüter (Produktionsmittel) benötigen und damit auch weniger nachfragen als früher, was ein Dominoeffekt auf dem Markt der Produktionsgüter (Investitionsgüter) in Gang setzen könnte. Dann würde die Produktion flächendeckend absinken. Das ist mit dem vorhin erwähnten Problem des ständigen Scheiterns der Investoren während der Depression gemeint. Nicht die Wirtschaftsakteure machen etwas falsch, sondern das Investieren „vernichtet“ das Einkommen.
Was tun? Um unsere Analyse fortsetzen zu können, nehmen wir einfach an, dass die Unternehmer des Sektors 3 die nicht absetzbaren Güter selber konsumieren. Dies lässt sich sinngemäß als Entsparen und Desinvestieren bezeichnen. Wir nehmen jetzt einfach an, der Sektor 3 bzw. seine Kapitaleigner sind bereit dies auch zu tun: Sie wollen einen Teil ihrer Amortisation (120) konsumieren - also entsparen bzw. desinvestieren. So etwas werden sie in einer richtigen Wirtschaft höchstwahrscheinlich nicht tun wollen, ja sogar nicht tun können, aber dazu kommen wir noch.
Diese kleine unrealistische Annahme hilft uns, in die Reproduktionsperiode 2 zu gelangen. Das bedeutet - weil es am Ende der vorigen Reproduktionsperiode so entschieden wurde -, dass der Sektor 2 am Anfang dieser Reproduktionsperiode seine Produktion mit mehr Kapital (120), der Sektor 3 dagegen mit weniger (-120) verfügt. Dies hat sich aus den produktionstechnischen Bedingungen ergeben, die wir in der Reproduktionsperiode zuvor hatten. Sie waren nämlich so, dass der Sektor 2 nur dann mehr Kapitalgüter erwerben (120) konnte, wenn der Sektor 3 auf die gleiche Menge verzichtete (-120). Man kann diese Situation durchaus als ein Nullsummenspiel betrachten. Mit zwei Tabellen lässt sich - wie bereits vorhin gehabt - darstellen, was in dieser Reproduktionsperiode t+2 geschehen wird.
| |
| t + 2 |
Produktionsprozess |
| |
| Sektor 1: |
| Sektor 2: |
| Sektor 3: |
|
| |
K |
|
Ÿ |
|
|
|
Y |
|
| |
2500.00 |
+ |
1000 |
|
= |
|
3500.00 |
|
| |
1620.00 |
+ |
1080 |
|
= |
|
2700.00 |
|
| |
1880.00 |
+ |
1880 |
|
= |
|
3760.00 |
|
|
|
|
| Kapitalbeschaffung |
| für Reproduktionsperiode t + 3 |
|
| |
K1t+3 |
= |
K1t+2 + 200 |
|
= |
|
2700.00 |
|
| |
K2t+3 |
= |
K2t+2 + 120 |
|
= |
|
1740.00 |
|
| |
K3t+3 |
= |
K3t+2 - 120 |
|
= |
|
1760.00 |
|
|
|
Die linke Tabelle schildert wieder den Produktionsprozess. Wir stellen fest, dass sich beim Sektor 1 offensichtlich immer noch nichts geändert hat. Der Sektor 2 wirtschaftet diesmal aber mit mehr Kapital (1620) als früher (1500). Es ist ein Zuwachs von 8%. Wir wollten vorerst die Einzelpreise der Güter nicht ändern, so dass wir auch die Nettoeinkünfte in diesem Sektor prozentual um den gleichen Wert erhöht haben (80). Dem Sektor 3 stand am Anfang weniger Kapital zur Verfügung (1880) als zuvor (2000). Für ihn bedeutete dies eine Desinvestition von 6%. Da auch die Preise der Konsumgüter weiterhin unverändert bleiben sollen, haben wir die Nettoeinkünfte bei ihm prozentual um den gleichen Wert verringert (120). Wenn dies alles berücksichtigt wird, dann ergeben sich die Werte der Produktion für alle drei Sektoren, so wie es die linke Tabelle darstellt.
Die rechte Tabelle beschreibt, wie die Produktionsgüter innerhalb der Sektoren distributiert werden. Darüber entscheiden die Wirtschaftsakteure. Wir wollen aber, dass sich das Wachstum fortsetzt, und zwar mit einem gleichen Tempo. Damit ist gemeint, dass der Sektor 2 auch diesmal seine Investitionen um die gleiche Summe (120) vergrößern (=1740) soll. Dem Sektor 3 wird dann zum Investieren das übrig bleiben, was der Sektor 1 nicht dem Sektor 2 bereits distribuiert hat, was noch weniger ist (-120) als in der vorigen Reproduktionsperiode (=1760). Was den Sektor 1 betrifft, da hat sich diesmal auch etwas geändert. Er kann jetzt sparen und investieren, und zwar real, weil der Sektor 2 im Laufe der betrachteten Reproduktionsperiode mehr Produktionsgüter (Rohstoffe und Halbfabrikate) hergestellt hat als vorhin (200).
Wenn wir mehr über das Gleichgewicht in dieser Reproduktionsperiode wissen wollen, müssen wir wieder die Tauschtabelle entwerfen. Wir haben gerade beschrieben, wie das geht, jetzt zeigen wir nur das Endergebnis.
Was stellen wir fest? Damit die Wirtschaft in der Reproduktionsperiode t+2 im Gleichgewicht bleibt, muss der Sektor 3 auch diesmal einen Teil seiner Produktion selber verkonsumieren - er muss also wieder entsparen und desinvestieren. Weil sich dies schon zum zweiten Mal wiederholt, ist dieses Ergebnis zumindest verwirrend. Kann es nämlich sein, dass die freie Marktwirtschaft gar nicht durch Sparen und Investieren wachsen kann? Da wir vorhin zahlenmäßig alles richtig gemacht haben, wäre diese Vermutung alles andere als abwegig. Sie stand schon am Anfang des nachfragetheoretischen Denkens. Nun ist es eine Tatsache, dass die Marktwirtschaften wachsen können. Deshalb schrieb Malthus:
„Sismondi bemerkt folgendes über die Grenzen der Kapitalsanhäufung: „Nach allem diesen muß man sagen, daß es niemals möglich ist, die Gesamtheit der Erzeugung des Jahres, gegen die Gesamtheit des vorhergehenden Jahres auszutauschen.“ Wenn dies wirklich zuträfe, so wäre es schwer zu erklären, wie der Wert des nationalen Einkommens überhaupt je steigen könnte.“

Mit dem Sayschen Gesetz sollte bewiesen werden, dass der Gedankengang der Nachfragetheoretiker prinzipiell falsch ist. Ein Jahrhundert später, nach der Großen Depression hat die Realität das Saysche Gesetz - wieder einmal - zur Farce gemacht. „Die Sparsamkeit ermöglicht eine hohe Akkumulationsrate und behindert gleichzeitig ihre Realisierung“ - hat es Joan Robinson auf den Punkt gebracht. Einerseits hat es zweifellos einen Sinn, heute zu investieren, damit später mehr produziert werden kann und damit auch mehr Arbeitsplätze entstehen. Andererseits, wenn man heute spart, wer wird dann heute die Güter kaufen, die schon hergestellt sind? Muss dann nicht doch ein Teil der Güter unverkauft bleiben?
Gerade dieses Dilemma des Sparens wollen wir mit Hilfe des Kreislaufsmodells auflösen. Eine Antwort kann uns auch unser konkretes numerisches Beispiel liefern, wenn wir es fortsetzen. Der Leser kann dies alleine tun. Weil es sich aber um eine reine Routine handelt, können wir uns diese Arbeit sparen. Es ist nämlich heute kein Problem jede Routine, wie kompliziert sie auch sein mag, programmiertechnisch zu realisieren. Wir können alle vorhin unternommenen Schritte als ein Algorithmus programmieren, der uns bequem ein fertiges Ergebnis liefert.
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|
|
|
|
|
|
| 480 |
 |
|
|
|
| 480 |
 |
|
|
|
| 800 |
| 480 |
 |
|
|
|
| 1120 |
| 480 |
 |
|
|
|
| 1440 |
| 480 |
 |
|
|
|
| 1760 |
| 480 |
 |
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| |
t+1 |
|
t+2 |
|
t+3 |
|
t+4 |
|
t+5 |
|
t+6 |
|
t+7 |
|
t+8 |
|
t+9 |
|
t+10 |
| |
| I1' |
-0
|
|
200
|
|
200
|
|
200
|
|
200
|
|
200
|
|
200
|
|
200
|
|
200
|
|
200
|
| |
| + |
| + |
| + |
| + |
| + |
| + |
| + |
| + |
| + |
| + |
| |
| I2' |
120
|
|
120
|
|
120
|
|
120
|
|
120
|
|
120
|
|
120
|
|
120
|
|
120
|
|
120
|
| |
| + |
| + |
| + |
| + |
| + |
| + |
| + |
| + |
| + |
| + |
| |
| I3' |
-120
|
|
-120
|
|
160
|
|
160
|
|
160
|
|
160
|
|
160
|
|
160
|
|
160
|
|
160
|
| |
|  |
|  |
|  |
|  |
|  |
|  |
|  |
|  |
|  |
|  |
| |
| ∑I' |
-0
|
|
200
|
|
480
|
|
480
|
|
480
|
|
480
|
|
480
|
|
480
|
|
480
|
|
480
|
| |
| S2 |
12%
|
|
11.1%
|
|
10.3%
|
|
9.7%
|
|
9.1%
|
|
8.6%
|
|
8.1%
|
|
7.7%
|
|
7.3%
|
|
7%
|
| |
Die dunkelgrünen Balken zeigen die Investitionen der Wirtschaft unseres Beispiels summarisch, unten sind die Anteile aller drei Sektoren einzeln angeführt. Wie wir schon festgestellt haben, hat Sektor 3 in den ersten zwei Reproduktionsperioden Absatzprobleme, so dass er aus seinem Amortisationsfonds konsumieren (entsparen) muss, was Deinvestieren bedeutet - also negative Investitionen (-120). Aber in den allen darauf folgenden Reproduktionsperioden können schon alle Sektoren aus ihrem Nettoeinkommen sparen und investieren, ohne dass damit das Gleichgewicht der Wirtschaft beeinträchtigt wäre. Das lässt sich noch besser verdeutlichen, wenn wir die obigen Zahlenreihen als Grafikdiagramm zeichnen.
| |
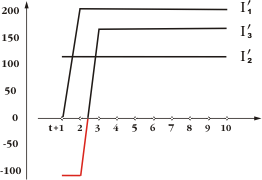 |
| Sektor 1 |
| Sektor 3 |
| Sektor 2 |
|
Das Sparen - und Investieren - vernichtet schon in der Reproduktionsperiode t+3 keine Nachfrage mehr. Hier ist es also zu einer Wende oder Umkehrung gekommen. Danach wächst die Wirtschaft immer weiter linear, und zwar mit einer immer gleichen absoluten Rate. Bei einem solchen Wachstum verringert sich die prozentuale Investitions- und Sparquote des Sektors 2 - und auch der ganzen Wirtschaft - fortlaufend. Am Anfang entsprach der Wert 120 beim Sektor 2 einem Zuwachs der Investitionen um 8% und der Sparquote von 12%, später wurden diese prozentuellen Größen immer kleiner. Wir könnten natürlich die Investitionsquote von 8% auch bei jeder nächsten Reproduktionsperiode beibehalten, dies würde dann ein exponentielles Wachstum ergeben. Der Leser wird dies selber prüfen können - mit dem Simulationstool unten.
Die hellgrünen Balken zeigen, wie sich der Konsum, in Bezug auf den stationären Zustand, (absolut) ändert. Er schrumpft zuerst. Das Sparen und Investieren verlangen vorübergehend eine Abstinenz, wie es schon die alten Ökonomen behauptet haben. Ihren tiefsten Stand hat die Konsumproduktion in der Reproduktionsperiode t+3 erreicht, danach wächst sie jede Periode linear um 320, obwohl auch weiterhin gespart und investiert wird - nominal gleich viel (480). Das bedeutet in der Tat, dass gleichzeitig gespart und immer mehr konsumiert wird. Dass uns die alten Ökonomen auch so etwas erzählt hätten, daran können wir uns nicht erinnern; von den neoliberalen Ökonomen würden wir so etwas erst recht nie hören. Ist also alles, was man uns zwei Jahrhunderte lang über die sparsamen Reichen erzählt hat, über ihr selbstaufopferndes Entsagen, damit sie den fleißigen Menschen in Lohn und Brot bringen, nur eine Lüge? Ja und nein. Wäre die Marktwirtschaft fähig ohne Abstürze zu funktionieren, dann würde das Wachstum Hand in Hand mit mehr Konsum gehen: also ohne Abstinenz. Aber die Marktwirtschaft stürzt immer ab, und da liegt der Hund begraben. Die periodischen Krisen vernichten im großen Stil das bereits akkumulierte Kapital - ab und zu hilft auch Krieg dabei -, so dass es danach wieder eine Weile dauert, während der Sparen mit (gesamtwirtschaftlicher) Askese erforderlich ist; bald wird aber wieder ein Sparen ohne Askese möglich, bis dann die Wirtschaft wieder zusammenbricht, und so dreht sich in der kapitalistischen Hölle alles weiter im Kreise. Diese Problematik werden wir bei den nächsten Phasen des ökonomischen Zyklus näher erörtern.