Marx hat nie einen Schritt in die dreckigen und dunklen Produktionshallen der Werkstätten seiner Zeit getan, er war sich aber trotzdem felsenfest sicher - zumindest bevor er beim Dritten Band des Kapitals angelangt war -, dass die dort verrichtete langweilige, mühevolle und gesundheitsruinierende Arbeit im Kommunismus das erste Bedürfnis und Vergnügen des Menschen sein würde. So sehr sollte sich nach der letzten Revolution der „menschlichen Geschichte“ das Bewusstsein der Menschen verändern. Auch Schumpeter hat keine Ingenieure und Erfinder besucht, um sich über ihre Arbeit zu erkundigen, trotzdem meinte er, über Innovationen alles zu wissen, was für einen Ökonomen wissenswert wäre - die ersparte Zeit konnte er sinnvoller bei den Wiener Prostituierten verbringen. Die Innovationen seien seiner Überzeugung nach ein zyklisches Phänomen, das zugleich einen dermaßen starken Einfluss auf die Wirtschaft ausübt, dass auch diese in ihrem Takt mitschwingen müsste. Und dies sollte der einzige Grund sein, warum die freie Marktwirtschaft nicht immer in einem Zustand der vollkommenen Ordnung bei voller Beschäftigung verbleibt.
Es sind also die Innovationen, die laut Schumpeter die Freiheit hindern, ihr wunderbares Werk zu verrichten, die Wirtschaft (und die Gesellschaft) in einen Zustand des perfekten Gleichgewichts zu bringen. Diese angebliche Fähigkeit der Freiheit, das Gleichgewichts zu schaffen, wird in der Walrasschen Theorie (Modell) des allgemeinen Gleichgewichts mathematisch streng „bewiesen“, so dass Schumpeter diese Theorie sein ganzes Leben für der Weisheit letzten Schluss gehalten hat. Deshalb war es für Schumpeter selbstverständlich, dass nur diese Theorie auch die Grundlage seiner Theorie der ökonomischen Zyklen sein konnte. Nun ist es aber bekanntlich so, dass in der Gleichgewichtstheorie die Zyklen und überhaupt jede ernsthaftere Störung der Marktwirtschaft nicht möglich ist. Die innere Logik schließt solche Muster kategorisch aus. Was tun? Schumpeter fiel in der Tat etwas ein, diesen logischen Widerspruch zu beseitigen: Die Gleichgewichtstheorie sei angeblich eine statische Theorie:
„Ja, der statische Charakter der Theorie gewann durch die neue Analyse noch wesentlich an Strenge und Klarheit. Keine Darstellung ist „statischer“ als die Leon Walras, in dessen Hand sich die Grundprinzipien der Theorie seit dem Beginn unserer Wissenschaft in strengster Form kristallisierten.“

Durch Innovationen sollte nun diese statische Gleichgewichtstheorie nicht ersetzt, sondern nur zu einer dynamischen weiterentwickelt werden, die dann auch das Phänomen ökonomische Zyklen erklären würde. Damit konnte Schumpeter diejenigen für sich gewinnen - oder besser gesagt nicht verlieren -, die sich schwer damit abfinden würden, dass er die attraktivste Schlussfolgerung der Theorie des allgemeinen Gleichgewichts, die ewige Harmonie, ablehnte bzw. ins Gegenteil verkehrte. Hier hat sich Schumpeter als würdiger Nachfolger der kontinentalen bzw. der deutschen Metaphysik erwiesen, die man immer leicht an dem berühmten Satz von Hegel erkennt: „Desto schlimmer für die Tatsachen!“ Es gebe angeblich tiefer liegende Wahrheiten über die Realität, die mit den Tatsachen nichts zu tun haben, und es gebe empirische Erkenntnisse. Die statische Theorie des allgemeinen Gleichgewichts sollte nach Schumpeter diese tiefere Wahrheit über die Funktionsweise der Marktwirtschaft in „strengster Form kristallisiert“ haben, mit den Innovationen würden man eine angewandte Wissenschaft betreiben. Da die Schumpetersche Innovationstheorie zugleich eine Theorie der ökonomischen Entwicklung darstellt, konnte sie für die Anhänger der kapitalistischen Wirtschaft sogar von großem Vorteil sein. Mit ihr konnten sie zum ersten Mal etwas in der Hand haben, was der damals so attraktiven Marxschen Theorie der historischen Entwicklung des Kapitalismus ein Schnippchen schlagen konnte.
Wenn die Theorie des allgemeinen Gleichgewichts beibehalten werden sollte, dann konnte als Ursache der ökonomischen Zyklen nur etwas in Frage kommen, das eine nichtökonomische Natur hat, also irgendwelcher sogenannter externer Faktor. Das wäre zum Beispiel der Fall mit den Sonnenflecken, für die sich der Stammvater des angloamerikanischen Neoliberalismus, Jevons, entschieden hat. Aber die Innovationen sind bei Weitem nicht so extern für eine Wirtschaft wie etwa die Sonnenflecken. Es gehört bekanntlich zum normalen Geschäft der Unternehmen, die Produktionsmethode ständig zu verbessern. Deshalb musste sich Schumpeter einiges einfallen lassen, um die Innovationen so weit wie es nur geht zu externalisieren, also sie von dem zu trennen, was man unter den internen Bewegungskräften der Marktwirtschaft verstehen sollte. Nur so kann man sich erklären, warum in seiner Innovationstheorie der ökonomischen Zyklen ein ganzes Ensemble von sehr seltsamen Annahmen zu finden ist. Erwähnen wir jetzt nur die wichtigsten.
Das neue technische Wissen sollte laut Schumpeter „schwarmweise“ auftreten, also in Wellen. Dieses Wissen sei dann angeblich allen, auf jeden Fall sehr vielen Unternehmern sofort bekannt und als solches für sie sofort frei verfügbar. Was also das neue technische Wissen betrifft, da sind die Unternehmen bestens informiert, aber in einer anderen Hinsicht sind sie es nicht. Sie wissen so gut wie nichts darüber, was ihre Konkurrenz so treibt - oder zumindest wollten sie davon nichts wissen. Sie verhalten sich auf einmal völlig irrational. Sobald das neue Wissen aufgetaucht ist, beginnen sie laut Schumpeter unverzüglich zu investieren, auch dann noch, wenn es schon allen klar sein müsste, dass im betreffenden Marktsegment schon zu viele Kapazitäten entstehen. Wenn alle Unternehmen gleich zu investieren angefangen haben, ist es für Schumpeter auch selbstverständlich, dass alle Investitionen gleichzeitig fertig sein werden. Die fertigen Investitionen werden also in einer kurzen Zeitspanne in Betrieb genommen, so dass dann die Wirtschaft durch riesige Disproportionalitäten im Bereich der Produktion zusammenbrechen muss.
Das sind nur die auffälligsten Annahmen, welche die Schumpetersche Dynamisierung der statischen Theorie ausmachen. Ohne sie würden die Innovationen in der „ewigen Harmonie“ der Gleichgewichtstheorie unauffällig untergehen. Ihretwegen würde man die üblichen logischen Schlussfolgerungen nicht revidieren müssen. Der Walrasche Unternehmer hat nämlich alle nötige Informationen darüber, wo und wann sich rentabel und sicher investieren lässt, so dass für ihn die innovativen Innovationen nicht mehr als nur eine reine Kostenfrage sind. Es gibt also keinen logischen Grund dafür, warum die Innovationen in dem statischen Modell Wellen verursachen sollten. Das Schumpetersche Ensemble von hirnrissigen Annahmen war der Preis für die Rettung der Gleichgewichtstheorie, auf Kosten der Realität. Wir wollen diese Annahmen nicht auf einmal einer kritischen Prüfung unterziehen, sondern wir werden es nacheinander tun - so wie es zu unserer Themenstruktur passt. Jetzt, bei der Untersuchung bzw. der Erklärung der Erholung, wollen wir uns nur die Annahme des „scharenweisen Auftretens“ des neuen technischen Wissens näher anschauen.
Schumpeter meinte sogar zu wissen, dass es nicht nur eine, sondern sogar drei Wellen gibt, welche die Wirtschaft zum Schwingen bringen. Er lässt uns auch wissen, dass all diese drei Wellen nicht er entdecken musste, weil dies schon die anderen - natürlich Ökonomen - getan haben. Es lag für ihn nahe, die Wellen nach ihren angeblichen Entdeckern zu benennen:
| Kitchin-Zyklus (3 bis 4 Jahre) |
Juglar-Zyklus (7 bis 11 Jahre) |
Kondratieff-Zyklus (50 bis 60 Jahre) |
| 1923 von J. Kitchin in den USA und Großbritannien festgestellt; Existenz umstritten. |
1860 von C. Juglar festgestellt; dieses ist der Konjunkturzyklus. |
Bis heute lassen sich Kondratjew-Zyklen allerdings statistisch nicht nachweisen. In der Volkswirtschaftslehre herrscht inzwischen ein breiter Konsens, der davon ausgeht, dass keine zyklischen Konjunkturmuster existieren, also auch der Kondratjew-Zyklus nicht. Nach der Meinung fast aller Makroökonomen folgt das Wirtschaftswachstum einer Zufallsbewegung.  |
Wie man die Wellen benennt, hat natürlich mit der Sache selbst so gut wie nichts zu tun. Trotzdem ist es nicht uninteressant zu fragen, warum diese Wellen einen Namen brauchten. Das was als Juglar-Zyklus benannt wird, ist nichts anderes als das, was man schon seit vielen Jahrzehnten schlicht als „ökonomischen Zyklus“ bezeichnete. Aber hinter dieser Benennung der Zyklen mussten doch irgendwelche Absichten stehen. Die Neoliberalen - zu denen auch Schumpeter gehört - würden sogar schwören, dass hinter jeder Handlung rationale Gründe stehen, darüber hinaus solche, die auf egoistischen Interessen beruhen. Desto mehr sind wir berechtigt, nach Schumpeters Absichten zu fragen. Wir werden es natürlich nie genau herausfinden können, aus welchen rationalen (und egoistischen) Überlegungen er so viel Großzügigkeit zeigt, wenn er die anderen zu Entdeckern der Wellen machte, aber es muss erlaubt sein, alle Möglichkeiten in Erwägung zu ziehen. Auch solche, die nicht sehr schmeichelhaft sind. Dann würde uns auch Folgendes einfallen: Wenn etwas problematisch sein könnte, ist man immer gut beraten, die Originalität der Entdeckung dem anderen „zuzuerkennen“.
Schumpeter konnte sich bestimmt gut vorstellen, dass Zweifel aufkommen werden, ob sich das technische Wissen wirklich zyklisch vorwärts bewegt, deshalb fragt man sich verlegen: Wäre es nicht schon schwierig genug, mit einer Welle zu Recht zu kommen? Warum prescht Schumpeter sofort mit drei vor? Auch hier dürfen wir nicht an reinen Zufall glauben, sondern eine rationale Erklärung dafür suchen. Und es muss wieder erlaubt sein, alles in Erwägung zu ziehen, ohne dass man sich den Vorwurf der Unterstellung gefallen lassen muss. Dann würde uns auch Folgendes einfallen: Könnte es etwa daran liegen, dass sich drei Wellen noch einfacher an die Realität anpassen lassen als etwa eine oder zwei? Auf den ersten Blick scheint ein solcher Gedanke völlig an den Haaren herbei gezogen zu sein. Aber der erste Blick hat uns schon des Öfteren getäuscht. Gehen wir dieser Problematik nach.
Hier kann uns vielleicht in Sinn kommen, dass wir von den Artisten gehört haben, dass mit mehreren Bällen einfacher zu jonglieren ist als mit nur wenigen. Für uns, die gar nicht jonglieren können, scheint dies völlig unverständlich zu sein. Leider haben wir gar keine Möglichkeit dies zu prüfen. Entweder schenken wir den Artisten den Glauben oder eben nicht. Deshalb versuchen wir die Frage, warum drei Wellen, anders zu enträtseln, und zwar mathematisch. Das „scharenweise“ Auftreten der Innovationen ist doch ein quantitatives Phänomen, und dafür ist nichts kompetenter als die Mathematik.
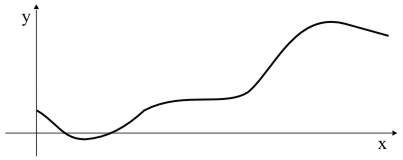
Wir wollen auch diesmal den Nichtmathematiker nicht überfordern. Es reicht wenn er sich nur daran erinnert, dass sich mathematische Funktionen graphisch darstellen lassen. Was wir in den folgenden zwei Bildern sehen, können also zwei Funktionen sein, dargestellt zwischen einer horizontalen x-Achse und einer vertikalen y-Achse.
 |
|
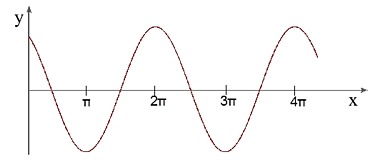 |
Im rechten Bild lässt sich unschwer eine elementare mathematische Funktion erkennen: eine Sinusfunktion. Sie ist sozusagen Inbegriff der Periodizität, ein Muster, das zur unmittelbaren Lebenserfahrung eines jeden Menschen gehört. In der Sinusfunktion wiederholt sich ein Abschnitt immer wieder - ähnlich wie bei den Wellen auf der Wasseroberfläche. In dem linken Bild werden wir dieses Muster der Periodizität offensichtlich nicht erkennen. Das ist schon ein wesentlicher Unterschied zwischen der rechten und der linken Funktion, wenn es sich im letzteren Fall überhaupt um eine Funktion handeln sollte. Auf jeden Fall haben wir es in dem linken Bild nicht mit einer elementaren mathematischen Funktion zu tun, also mit einer, die sich mit Hilfe der üblichen mathematischen Operatoren (Symbolen) als Formel schreiben lässt. (Dies könnte eine Sammlung der empirischen, statistisch erfassten Daten sein.) Wir stellen uns jetzt die Frage, ob die Funktion links etwas mit dem zu tun haben könnte, was rechts dargestellt ist. Ein mathematisch begabter Abiturient würde uns selbstbewusst und stolz erklären, dass die linke - nennen wir es bedingt - Funktion nichts, aber gar nichts mit der rechten zu tun hat. Stimmt das aber?
Jean Baptiste Joseph Fourier (1768-1830) war ein französischer Mathematiker und Physiker. Er zeigte in seiner mathematischen Arbeit, dass sich jede Funktion, wie unregelmäßig und unperiodisch sie auch verlaufen mag, aus periodischen, harmonischen Schwingungen zusammensetzen lässt, also aus Sinusfunktionen, die eine verschiedene Phase, Amplitude und Frequenz haben. Diese Umwandlung ist als Fourier-Transformation bekannt. (Im Internet kann man über sie Näheres erfahren.) Auf den Punkt gebracht: Jede Funktion und damit auch eine Sammlung von Daten im kartesischen Koordinatensystem lässt sich in eine (theoretisch unendliche) Menge von Sinusfunktionen zerlegen. Wie viele Sinusfunktionen wir in einem konkreten Fall brauchen, hängt nur davon ab, wie kompliziert die unregelmäßige Funktion bzw. der Verlauf der Daten ist und wie genau wir es haben wollen. Manchmal lässt sich mit nur einer kleinen Zahl von Sinusfunktionen eine gute Annäherung erzielen.
Wenn wir jetzt an die drei Wellen von Schumpeter denken, leuchtet uns etwas ein. Eine empirische Sammlung von Daten, die einander einer Zeitachse entlang zugeordnet sind, wie auch immer diese Sammlung aussehen mag, lässt sich mit drei Wellen viel einfacher „erklären“ als nur mit einer. Wenn man es will, kann man sich diese so paradox klingende Transformation auch so verdeutlichen: Wenn sich zum Beispiel nach 6 Jahrzehnten kein Kondratjew-Hochstand bemerkbar macht, kann man ihm einen Juglar-Tiefstand unterschieben und schon passt die Theorie deutlich besser zu den Tatsachen als davor. Und nun man kann auch noch mit dem kleinen Kitchin nachkorrigieren.
Denkt man über die praktische Nutzung der Fourier-Transformation nach, kommt einem noch etwas in Sinn. Was die Mathematik hier tut, wird in den verbalen Argumentationen mit Ad-hoc-Hypothesen gemacht. Mit einer zusätzlichen Ad-hoc-Hypothese kann man immer die letzte Aussage (Schlussfolgerung) so beeinflussen bzw. „nachbessern“, dass sie dem entspricht, was man vorher haben wollte. Man nennt das in der Philosophie und der Logik auch unendlicher Regress. Deshalb sind die Theorien, welche die Tatsachen ex post, aber nicht im Voraus erklären können, wertlos und damit auch keine seriöse Wissenschaft.
Wenn wir über die empirischen Tatsachen sprechen, was sollten diese in unserem Fall konkret sein? Was sind Innovationen bzw. neues technisches Wissen? Wollen wir die Schumpetersche Innovationstheorie prüfen, müssen wir genau das zuallererst klären. Aber da stoßen wir sofort auf eine Schwierigkeit. Schumpeter spaltet den Begriff Innovationen bzw. technisches Wissen in zwei Unterbegriffe. Es gibt für ihn die sogenannten Basisinnovationen bzw. Basiserkenntnisse und die restlichen Innovationen bzw. Erkenntnisse. Nach welchem Kriterium man klassifizieren soll, wurde uns aber nie erklärt. So landen wir auch in dieser Hinsicht auf einem Basar der Beliebigkeiten. Schauen wir uns etwa die Kondratjew Zyklen konkret an.
| |
1. Periode (ca. 1780–1849): |
Frühmechanisierung; Beginn der Industrialisierung in Deutschland; Dampfmaschinen-Kondratjew. Es gibt Vermutungen, dass es in England schon einen früheren Zyklus gab. |
| |
2. Periode (ca. 1840–1890): |
Zweite industrielle Revolution Eisenbahn-Kondratjew (Bessemerstahl und Dampfschiffe). In Mitteleuropa Gründerzeit genannt. |
| |
3. Periode (ca. 1890–1940): |
Elektrotechnik- und Schwermaschinen-Kondratjew (auch Chemie). |
| |
4. Periode (ca. 1940–1990): |
Einzweck-Automatisierungs-Kondratjew (Basisinnovationen: Integrierter Schaltkreis, Kernenergie, Transistor, Computer und das Automobil). |
| |
5. Periode (ab 1990): |
Informations- und Kommunikations-Technik-Kondratjew (Globale wirtschaftliche Entwicklung). |
Für das Industriezeitalter haben Eisen bzw. Stahl zweifellos sehr große Bedeutung. Wenn man verfolgt, wie sich das Wissen über Eisen und Stahl entwickelte, kann man Folgendes feststellen. Der zweite Kondratjew hat sich offensichtlich verspätet, da das Bessemer-Verfahren viel früher entdeckt wurde (1819). Von diesem Zeitpunkt an gerechnet kam aber das Siemens-Martin-Verfahren (1856) der Stahlerzeugung schon nach etwa einem halben Kondratjew. Sollte ein Kondratjew nicht diese beiden revolutionären Entdeckungen erfassen? Ein weiteres, das sehr wichtige Linz-Donawitz-Verfahren (Sauerstoffblasverfahren) benötigte sogar anderthalb Kondratjew-Zyklen (1949). Oder, wenn man die Kernenergie nimmt, so sind ihre theoretischen Grundlagen schon viel früher gelegt, als der angebliche 4. Kondratjew begonnen hat. Die Einführung der Elektrizität und des Automobils den Wellen anzupassen, ist ebenfalls schwierig. Sollte jetzt eine Umstellung auf Elektroautos und Solarenergie kommen, würde dies auch deutlich mehr als einen Kondratjew darstellen.
Bei den kürzeren Wellen ist dieses Schubladendenken noch weniger überzeugend. Um nicht zu tief in die Geschichte zu gehen, fragen wir etwa, welche Basisinnovation es bei den Programmiersprachen gab. War die Sprache Fortran eine Basisinnovation, aber Pascal und Cobol nicht? War es C++ oder Java - oder gar keine von ihnen? War die Windowsversion 3 eine revolutionäre Entdeckung, die 98 nur eine Weiterentwicklung und XP wieder revolutionär?
Die Innovationstheorie von Schumpeter kann uns also gar nichts über die Zukunft sagen. Sie ist praktisch nutzlos. Nutzlos? Es hängt aber davon ab, was unter nutzlos verstanden wird. Die Innovationstheorie hat eine klare weltanschauliche Botschaft, und zwar dass wir gegen die Krisen der Marktwirtschaft nichts unternehmen können, so dass wir sie als unser hartes aber unabwendbares Schicksal hinnehmen sollten. Eine bessere Welt sei nicht möglich.
Ob Schumpeter selbst an seine Erklärung der ökonomischen Zyklen glaubte? Sogar das lässt sich bezweifeln. In seinem letzten wichtigen Werk Kapitalismus, Sozialismus und Demokratie - danach hat er sich nur mit der Geschichte beschäftigt - steht nämlich:
Ich meine, dass eigentlich das zu hohe Niveau der amerikanischen Löhne immer, und vor allem in den dreißiger Jahren, die wichtigste Ursache der Arbeitslosigkeit in den Vereinigten Staaten war, und dass ähnliche Folgen auch in der Zukunft zu erwarten sind, wenn man die Politik der hohen Löhne fortsetzt.
Von der dynamischen Weiterentwicklung mit Hilfe von Innovationen ist also nichts übrig geblieben. Die statische Theorie hat letztendlich die dynamische versenkt. Aus empirischer Sicht hatte die innovative Theorie der Zyklen erst recht versagt. Wenn man nämlich bedenkt, dass wir drei Jahrzehnte nach dem Weltkrieg keinen ökonomischen Absturz, also keine mittleren Wellen hatten, kann man folgern, dass die Unternehmen keine große Disproportionalität verursachen. Und dies war bekanntlich eine Zeit, als die Produktivität so schnell wuchs, wie nie davor und danach. Wenn am Ende des 20. Jahrhunderts der neue Kondratjew beginnen sollte, müssten wir in den letzten Jahren ein neues Wirtschaftswunder erleben, stattdessen haben wir so etwas wie eine Große Depression bekommen (2008). Die angeblich technisch überforderten Unternehmen sind reine akademische Spekulation - noch besser gesagt Spinnerei.
Schumpeter war in der Tat eine tragische Figur, wie es Jürg Niehans feststellte, aber nicht ohne eigene Schuld. Er wollte eine originelle Idee auf die Grundlage einer unsinnigen Theorie stellen, und das war nicht möglich. Eine Idee, möge sie auch noch so gut sein, passt nicht in jedes „System von Gedanken“ (Kant) oder Paradigma. Das partikel-mechanische Modell der Marktwirtschaft ist nicht das richtige für die Idee von Innovation, sondern das Kreislaufmodell, wie wir gesehen haben. Im analytischen Rahmen dieses Modells schaffen die Vorsprungsprofite die für den Aufschwung nötige Nachfrage. Später werden wir zeigen, dass das Verschwinden solcher Profite die Wirtschaft zum Absturz bringen wird, auch wenn die praktischen Unternehmer nicht die geringsten Disproportionalitäten während der Hochkonjunktur verursacht hätten. Nicht die Disproportionalitäten, sondern wieder die Nachfrage, die verloren gegangene Nachfrage, führt zu ökonomischen Krisen.
Und noch einen guten Einfall hatte Schumpeter, nämlich seine Kredittheorie. Aber auch hier fehlte ihm der richtige analytische Rahmen, so dass er ständig logische Widersprüche produzierte und mit der Realität kollidierte. Wir schauen uns jetzt an, was sich mit den Krediten bzw. schuldenfinanzierten Investitionen im Rahmen des Kreislaufmodells machen lässt.