| |
|
 |
|
| |
| |
B - Das Sparen und das allgemeine Gleichgewicht der Marktwirtschaft |
| |
Die allgemeine Gleichung des Sparens und das Preisniveau der Produktionsgüter |
| |
|
|
|
| |
|
Es zeigt sich, dass die angeblich »evidente« Nachfragekurve, die mit steigendem Warenpreis zu fallen habe, sich auf Märkten ... keineswegs so verhalten muss, wie die neoklassische Lehrbuchweisheit verkündet: Im Gegenteil, der Fall, in dem die Nachfrage mit steigenden Preisen steigt ist viel wahrscheinlicher als der umgekehrte Fall, den die Neoklassik als Standard behauptet. |
|
| |
|
Michael R. Krätke, Neoklassik als Weltreligion? |
|
|
|
|
|
Unser illustratives Beispiel mit den Bauern, die Weizen anbauen, war zwar denkbar einfach; es ist uns trotzdem gelungen, mit seiner Hilfe einer Gesetzmäßigkeit zwischen bestimmten makroökonomischen Größen (Aggregaten), die wir als allgemeine Gleichung des Sparens bezeichnet haben, auf die Spur zu kommen. Dieses Ergebnis war jedoch nur mit gewagten Einfällen zu erreichen. Wir mussten uns nämlich Annahmen bedienen, die uns die Realität nie einräumen würde. Eine Eingut-Wirtschaft ist eine reine Fiktion, und dass es in einer solchen Wirtschaft auch noch Tausch und Markt geben sollte, ist schon eine ordentliche Absurdität. Es blieb uns aber nichts anderes übrig, wenn wir die Weizenmengen in Preisen erfassen wollten. Diese seltsamen Annahmen ließen sich deshalb entschuldigen, weil wir mit unserem Beispiel nur etwas veranschaulichen wollten. Für eine richtige Begründung unserer Schlussfolgerungen und ihrer endgültigen Beweise sind zweifellos stärkere analytische Mittel nötig - das haben wir unmissverständlich eingeräumt. Zu diesen Mitteln gehört das Kreislaufmodell mit seinen distributiven und technischen Koeffizienten, das wir in den vorigen Beiträgen in dessen Hauptzügen vorgestellt haben. Das Modell würde bei leidenschaftlichen Mathematikern das Herz höher schlagen lassen, wir sind aber der Mathematisierung des Modells vorerst ausgewichen, indem wir uns eines numerischen Beispiels bedient haben. Mit diesem Beispiel wird es uns gelingen, zu manchen weiteren relevanten Ergebnissen zu kommen. Sie werden sich später mit rein mathematischen Mitteln überprüfen lassen, womit ihre allgemeine Gültigkeit endgültig nachgewiesen sein wird.
Dieses Ergebnis war jedoch nur mit gewagten Einfällen zu erreichen. Wir mussten uns nämlich Annahmen bedienen, die uns die Realität nie einräumen würde. Eine Eingut-Wirtschaft ist eine reine Fiktion, und dass es in einer solchen Wirtschaft auch noch Tausch und Markt geben sollte, ist schon eine ordentliche Absurdität. Es blieb uns aber nichts anderes übrig, wenn wir die Weizenmengen in Preisen erfassen wollten. Diese seltsamen Annahmen ließen sich deshalb entschuldigen, weil wir mit unserem Beispiel nur etwas veranschaulichen wollten. Für eine richtige Begründung unserer Schlussfolgerungen und ihrer endgültigen Beweise sind zweifellos stärkere analytische Mittel nötig - das haben wir unmissverständlich eingeräumt. Zu diesen Mitteln gehört das Kreislaufmodell mit seinen distributiven und technischen Koeffizienten, das wir in den vorigen Beiträgen in dessen Hauptzügen vorgestellt haben. Das Modell würde bei leidenschaftlichen Mathematikern das Herz höher schlagen lassen, wir sind aber der Mathematisierung des Modells vorerst ausgewichen, indem wir uns eines numerischen Beispiels bedient haben. Mit diesem Beispiel wird es uns gelingen, zu manchen weiteren relevanten Ergebnissen zu kommen. Sie werden sich später mit rein mathematischen Mitteln überprüfen lassen, womit ihre allgemeine Gültigkeit endgültig nachgewiesen sein wird.
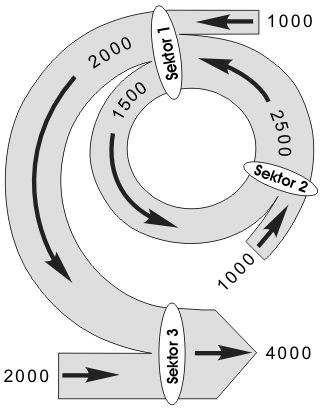
Unser numerisches Beispiel ist diesmal so aufgebaut, dass es sozusagen eine richtige Wirtschaft im Kleinformat darstellt, in dessen Rahmen die Produktion, der Tausch, das Wachstum und einiges mehr im üblichen Sinne des Wortes stattfinden können. Allgemein ausgedrückt, kann man innerhalb dieses Beispiels strukturelle Änderungen simulieren, die das Wichtigste, was in einer echten Wirtschaft passiert, erfassen. In diesem Beitrag wollen wir aber nur Preise ändern, um herauszufinden, was geschehen muss, wenn das Gleichgewicht der Wirtschaft weiterhin bewahrt werden soll. Um nicht „zurückblättern“ zu müssen, stellen wir unser - bereits mehrere Male benutztes - numerisches Standardbeispiel noch einmal als Flussdiagramm dar.
| |
|
 |
| Distributive Koeffizienten: |
| δ |
|
1 |
2 |
3 |
| |
|
Sektor 1 |
Sektor 2 |
Sektor 3 |
| 1 |
Sektor 1: |
0 |
3/7 |
4/7 |
| 2 |
Sektor 2: |
1 |
0 |
0 |
| 3 |
Sektor 3: |
0 |
0 |
0 |
|
|
Zum besseren Verständnis könnte es nützlich sein, wenn wir uns die dargestellte Wirtschaft so vorstellen, dass der Sektor 2 Eisen, der Sektor 1 Maschinen und der Sektor 3 Konsumgüter herstellt. Die externen Inputs der Sektoren stellen verschiedene Leistungen bzw. dafür ausbezahlte Einkünfte (Löhne, Sondervergütungen, Profite, Dividenden, Zinsen, ...) dar, die wir im Folgenden als Nettoeinkünfte bezeichnen.
Das allgemeine Gleichgewicht bei Preisänderungen - Inflation und Deflation
Wenn sich die Preise ändern, kann sich in der realen Wirtschaft vieles ändern. Dies kann sogar produktionstechnische Disproportionalitäten („Friktionen“) verursachen. Aber so weit wollen wir jetzt nicht gehen. In unserem numerischen Beispiel soll die produktionstechnische Struktur auch nach den Preisänderungen unverändert bleiben. Es sollen also weiterhin gleiche Güter in gleichen Mengen mit gleichen Produktionsmethoden hergestellt werden. Für unsere weitere Untersuchung ist es auch besonders wichtig, dass alle Einkünfte vollständig und unverzüglich ausgegeben werden. Damit wollen wir von vornherein ausschließen, dass Ungleichgewicht bzw. Nachfragemangel durch Nichtkonsumieren verursacht werden kann - etwa durch Geldhortung. Kurz gefasst, es sollen sich bei unserer weiteren Untersuchung nur Preise ändern und sonst nichts.
Wir gehen jetzt von dem stationären Zustand aus, der im obigen Flussdiagram dargestellt ist. Im ersten Schritt sollen die Preise in der Reproduktionsperiode t+1 steigen, und zwar bei jedem Sektor genau um 2%. Aus dem Flussdiagramm lässt sich unmittelbar entnehmen, wie danach die Produktion und die Preisbildung bei den Sektoren aussehen werden.
| |
| t +1 |
Produktionsprozess |
| |
| Sektor 1: |
| Sektor 2: |
| Sektor 3: |
|
| |
K |
|
Ÿ |
+ 2 % |
Teuerung |
|
Y |
|
| |
2500.00 |
+ |
1000 |
+ |
70 |
= |
3570.00 |
|
| |
1500.00 |
+ |
1000 |
+ |
50 |
= |
2550.00 |
|
| |
2000.00 |
+ |
2000 |
+ |
80 |
= |
4080.00 |
|
|
|
|
| Kapitalbeschaffung |
| für Reproduktionsperiode t +2 |
|
| |
K1t+2 |
= |
δ21 |
• |
Y2t+1 |
= |
1 • 2550.00 |
= |
2550.00 |
|
| |
K2t+2 |
= |
δ12 |
• |
Y1t+1 |
= |
3/7 • 3570.00 |
= |
1530.00 |
|
| |
K3t+2 |
= |
δ13 |
• |
Y1t+1 |
= |
4/7 • 3570.00 |
= |
2040.00 |
|
|
|
|
Die rechte Tabelle zeigt, wohin die Sektoren 1 und 2 ihre Produktion liefern bzw. in welchen Mengen. Mit dieser Distribution der Produktionsgüter wird erreicht, dass sich in der Wirtschaft real nichts ändert. Solche Situationen, bei denen sich die Preise ändern aber produktionstechnisch alles gleich bleibt, haben wir schon gehabt und untersucht. Von großer Hilfe waren dabei die distributiven Koeffizienten. Man kann auf diese Koeffizienten vor allem dann nicht verzichten, wenn man eine Wirtschaft als mathematisches Gleichungssystem schreiben will. Weil aber unser Fall jetzt sehr einfach ist, brauchen wir die distributiven Koeffizienten nicht explizit zu benutzen, aber man soll sich von ihnen trotzdem nicht verwirren lassen. Sie bedeuten nämlich nicht mehr, als dass in unserem Beispiel der Sektor 2 seine ganze Produktion dem Sektor 1 liefert und dieser die seinige den Sektoren 2 und 3 im Verhältnis 3/7 zu 4/7. Diese Daten lassen sich aus dem obigen Flussdiagramm unmittelbar entnehmen und werden rechts davon tabellarisch dargestellt. Dies aber nur nebenbei.
Haben die Sektoren 2 und 3 am Ende der Reproduktionsperiode t+1 ihre Güter tatsächlich nach diesen Verhältnissen (distributiven Koeffizienten) distribuiert, dann werden alle drei Sektoren in der nächsten Reproduktionsperiode t+2 zweifellos gleiche Mengen von Gütern herstellen wie zuvor. Dies lässt sich problemlos begreifen, wenn man sich nur ein bisschen in die produktionstechnischen Zusammenhänge des Beispiels hineindenkt. Aber in einer Marktwirtschaft geht es um Kaufen und Verkaufen, und wenn wir auch das mitzudenken versuchen, wird alles viel komplizierter. Obwohl unser dreisektorales numerisches Beispiel fast peinlich einfach ist - zumindest verglichen mit dem, was in der richtigen Wirtschaft passieren kann -, sind wir trotzdem nicht mehr im Stande, all diese Transaktionen und Zusammenhänge in unserem Gehirn zu erfassen und zu durchschauen. Es gibt aber zum Glück für solche Fälle, wenn die Datenmenge zu groß ist, Hilfsmittel, mit denen wir unsere Gedanken ordnen können. Tabellen sind bekanntlich auch eines dieser Hilfsmittel. Die Tabelle, die wir jetzt benutzen werden, können wir Tauschtabelle nennen. Sie ist zugleich eine Möglichkeit, um auf Mathematik (Gleichungssysteme) zu verzichten.
Wir werden jetzt eine Tauschtabelle für die konkreten Werte unseres Beispiels erstellen. Sie soll den Tausch am Ende der Reproduktionsperiode t+1 auf allen Ebenen erfassen. Zuerst tragen wir in diese Tabelle die Werte ein, die uns bisher bekannt sind - die sich aus dem vorigen Bild entnehmen lassen. Unsere bisherigen Überlegungen lassen uns wissen, welche Felder in unserer neuen Tabelle nicht leer sind, auch wenn wir ihre Werte noch nicht kennen. Wir markieren diese Felder vorerst mit einem Fragezeichen.
Bleiben wir bei der Annahme, dass die Wirtschaft auch weiterhin auf allen ihren Ebenen im Gleichgewicht bleibt, lassen sich die unbekannten Werte für die markierten Felder eindeutig bestimmen. Wenn nämlich die Sektoren 1 und 2 ihre restlichen Einkünfte für den Kauf der Konsumgüter des Sektors 3 ausgeben, so gibt es nur je einen in Frage kommenden Wert für die obigen zwei Felder in der Spalte 6. Es lässt sich leicht ersehen, dass diese Spalte das Angebot des Sektors 3 darstellt. Was die Sektoren 1 und 2 von der gesamten Produktion (4080) nicht kaufen, muss schließlich der Sektors 3 - der Konsumgüterhersteller - selbst verbrauchen. Daraus ergibt sich der Wert des untersten Feldes der Spalte 6. Des Weiteren stellen wir fest, dass die Spalte 6 identisch mit der linken Hälfte der Zeile 3 ist, so dass wir jetzt alle Felder ausgefüllt haben. Nun können wir die Tauschtabelle vervollständigen und die restlichen Werte ausrechnen.
Stellen wir noch einmal ausdrücklich heraus, was die Werte in der linken Hälfte der Zeile 3 bedeuten: Es sind Ausgaben für die Konsumgüter aller drei Sektoren. Die Zeile 4 stellt die Nettoeinkünfte aller drei Sektoren dar. Zieht man jetzt diese Zeile von der vorigen ab, bekommt man Ersparnisse bzw. Investitionen der einzelnen Sektoren. Diese Differenz steht in der Zeile 5. Aus Gründen, die wir noch erörtern werden, ist für uns nur die Gesamtsumme der Ersparnisse bzw. der Investitionen interessant. Sie beträgt 120.
Wir schauen uns jetzt noch einmal die Sektoren 1 und 2 an, welche die Produktionsgüter herstellen. Vor der Preissteigerung - die Reproduktionsperiode t - war der Wert der von ihnen hergestellten Güter 3500 bzw. 2500, und danach - in der aktuellen Reproduktionsperiode t+1 - ist er auf 3570 bzw. 2550 gestiegen. Das ist eine summarische Steigerung von 120. Nun haben wir drei Größen, die wir jetzt nebeneinander stellen:
|
|
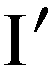 |
 |
|
120 |
120 |
120 |
Wenn wir dazwischen noch Gleichheitszeichen einfügen, haben wir eine erweiterte Gleichung bekommen, die wir schon bei unserem Beispiel mit den Weizen anbauenden Bauern als allgemeine Gleichung des Sparens bezeichnet haben.
Dem interessierten Leser ist es überlassen zu prüfen, dass diese Gleichung ihre Gültigkeit auch dann behält, wenn die Preise nicht bei allen Sektoren gleichmäßig steigen würden, wenn die Preise fallen würden, sowie bei jeder anderen Kombination, bei der bestimmte Produktionsgüter sich verteuern und die anderen sich verbilligen würden. Es geht natürlich immer nur um die Preise der Produktionsgüter, die der Konsumgüter werden bei der allgemeinen Gleichung des Sparens nicht berücksichtigt.
Das nominale und das reale Sparen bei den Preisänderungen
Wir haben bereits angedeutet, dass man die Ersparnisse der Sektoren nur als Summe betrachten soll. Dies hat damit zu tun, dass es letztendlich nicht die Sektoren sind, die sparen, sondern es sind immer die einzelnen Empfänger der Nettoeinkünfte. Diese können eine bestimmte Sparsumme S′ in unendlich vielen Kombinationen einsparen. Auch in unserem konkreten Fall können einige Einkommensbesitzer viel sparen, anderen nicht so viel und es wird bestimmt auch solche geben, die nichts sparen oder sogar über ihren Verhältnissen leben, aber bei der Preissteigerung von 2%, muss unterm Strich die Summe 120 herauskommen. Dann werden unsere Schlussfolgerungen immer ihre Gültigkeit behalten. Es ist interessant darüber nachzudenken, was diejenigen, die sparen, über das Sparen denken.
Stellen wir uns einen ganz normalen Sparer vor. Er hat keinen Überblick darüber, was in der Wirtschaft passiert. Er kennt nicht das Ganze, sondern nur sein Nettoeinkommen und er weiß, dass nur er alleine darüber entscheiden darf und kann, welche Bedürfnisse er befriedigen will und wie viel er einsparen wird. Deshalb ist es für ihn selbstverständlich, dass sich der Konsum und das Sparen gegenseitig ausschließen, dass das eine Vergnügen (Genuss) und das andere Verzicht (Abstinenz) bedeutet. Weil er für sein Einkommen etwas geleistet hat, ist er felsenfest auch davon überzeugt, dass er mit seinem Sparen dem zukünftigen Gläubiger eine bestimmte Leistungsmenge abgetreten hat. Das ist die Denkweise des individuellen Sparers. Bis dahin ist sie zumindest nicht ganz falsch. Der Sparer - abgesehen von seltenen Ausnahmen - wird es aber auch für selbstverständlich halten, dass alles, war für ihn als Individuum stimmt, auch für alle Individuen zusammen genommen stimmen muss und damit schließlich auch für die ganze Wirtschaft. Aber wie kann dies stimmen?
Auch wenn die individuellen Sparer bei uns konkret die Summe 120 eingespart haben, haben sie nicht weniger konsumiert als davor, als sie gar nichts eingespart haben. Den individuellen Sparern ist es natürlich klar, dass die Preise um 2% gestiegen sind, aber hätten sie auch dies gebührend berücksichtigt und ihre Sparsumme dementsprechend auf 117,4 herunter korrigiert, wäre auch dies kein realer Wert ihres Sparens. Man kann es drehen und wenden, wie man es will, das reale Sparen bleibt während der Reproduktionsperiode t+1 gleich Null.
Unsere Untersuchung lässt uns also in aller Deutlichkeit erkennen, dass das nominale und reale Sparen zwei völlig unterschiedliche Größen sein können. Bei unserem numerischen Beispiel lassen sich, genau genommen, drei von vier Merkmalen, durch die sich dieser Unterschied äußern kann, feststellen:
- Das nominale Sparen muss nicht bedeuten, dass real weniger Güter konsumiert werden.
-
Man kann den Konsum steigern, ohne dass man zuerst für eine bestimmte Zeit auf den Konsum verzichtet.
- Das nominale Sparen sagt nichts über die Änderungen im realen Kapitalstock (Kapitalakkumulation) aus.
- Den nominalen Ersparnissen muss keine produktive Leistung innewohnen.
Heißt es jetzt, dass die Realität verrückt spielt? Nein. Es handelt sich hier nur um einen Denkfehler, der die Folge dessen ist, dass man die wichtigsten Zusammenhänge nicht berücksichtigt hat: ein typischer Fehler der Pars-pro-toto-Denkweise. Diese schlechte Gewohnheit der Liberalen, mikroökonomische Schlussfolgerungen einfach linear auf makroökonomische Verhältnisse zu übertragen, wurde früher vor allem von dem deutschen Nationalökonomen Friedrich List (1789-1846) heftig kritisiert:
„Wie? Die Weisheit der Privat-Oekonomie say auch Weisheit in der National-Oekonomie? ... Nein! in der National-Oekonomie kann Weisheit sein, was in der Privat-Oekonomie Torheit wäre und umgekehrt, aus dem ganz einfachen Grunde, weil ein Schneider keine Nation und eine Nation kein Schneider ist; weil eine Familie etwas ganz Anderes ist, als ein Verein von Millionen Familien, ein Haus etwas ganz Anderes, als ein großes National-Territorium.“

Wie Recht er hatte. Die Wirtschaft ist kein großes Unternehmen oder ein großer Haushalt. Beim Sparen wird dies nur besonders deutlich.
Die Preisänderungen und das Gleichgewichtsproblem
Nachdem in unserem Beispiel die Preise um 2% gestiegen sind, kommt das Gleichgewicht nur dann zustande, wenn die Investitionen nominal um 120 steigen, und genau soviel muss auch eingespart werden. Es lässt sich unschwer ausrechnen, dass bei einer Preissteigerung von 4% die Spar- und Investitionssumme auf 240 steigt und bei der Deflation von 2% auf minus 120 fällt. Das ist mit den Balken in dem nächsten Bild anschaulich dargestellt. Würden wir die Preisänderung in ganz kleinen (infinitesimalen) Schritten berechnen, bekommen wir eine Linie, die auch eingezeichnet ist. Das Bild als Ganzes stellt eigentlich eine grafische Darstellung der allgemeinen Gleichung des Sparens für unser numerisches Beispiel dar, wenn sich das Preisniveau ändert.
| |
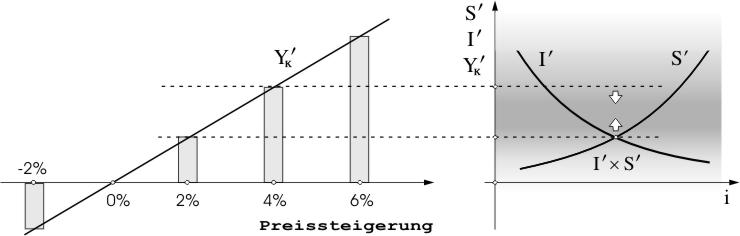 |
Die rechte Seite der Grafik schildert das Gleichgewicht zwischen den Ersparnissen und Investitionen, das wir bereits als spezielle Gleichgewichtsbedingung bezeichnet haben. Dass die Wirtschaft nicht im Gleichgewicht sein kann, wenn sich die Ersparnisse nicht den Investitionen angleichen, dem würden sogar die Angebotstheoretiker beipflichten. Sie würden aber sofort hinzufügen, dass der Zins eine Kraft ist, die Investitionen (I) und Ersparnisse (S) zum Ausgleich bringt. Wenn wir schon über das Sparen sprechen, sollte auch diese angebotstheoretische Auffassung kurz erläutert werden.
Nehmen wir an, die Wirtschaft befindet sich im Ungleichgewicht, da mehr gespart als investiert worden ist. Wenn die Neigung zum Sparen größer ist als die zu Investitionen, wird der Zinssatz fallen, weil das Geldangebot größer als seine Nachfrage ist. Einerseits geht demzufolge die Neigung zum Sparen zurück, andererseits sind die Unternehmer wegen des billigeren Geldes bereit, mehr zu investieren. Diese Kräfte wirken dann so lange, bis sich Ersparnisse und Investitionen irgendwann ausgleichen. Wenn umgekehrt die Neigung zum Sparen kleiner als die zu Investitionen ist, weshalb der Zinssatz steigt, gleichen sich Sparen und Investitionen ebenfalls aus; hier läuft die Anpassung aber auf genau umgekehrte Weise. So die Theorie.
Die hartnäckigsten Ankläger gegen diese Erklärung sind die empirischen Tatsachen. Man findet kaum überzeugende Beispiele aus der Geschichte, wo mit höheren Zinsen das Wachstum verlangsamt und mit niedrigeren Zinsen angespornt oder beschleunigt wurde. Fast immer war es genau umgekehrt. Den Japanern ist es zum Beispiel jahrzehntelang nicht gelungen, mit extrem niedrigen Zinsen den Aufschwung herbeizuführen. Man hat auch oft beobachtet, dass eine Depression mit Unterauslastung der Produktionskapazitäten und hoher Arbeitslosigkeit noch lange fortdauerte, nachdem die Zinsen praktisch auf Null abgesenkt wurden. Es nützt der Wirtschaft also wenig, wenn das Zinsniveau sinkt und es sich wegen der fallenden Kosten lohnen würde zu investieren, wenn die gesamtwirtschaftliche Sparquote weiterhin auf ungefähr gleichem, das heißt auf zu hohem Niveau bleibt. „Wer die Praxis beobachtet, wird sagen können, daß kein Moment die Spartätigkeit weniger beeinflußt als die Zinshöhe“, stellte zum Beispiel der Frankfurter Bankdirektor Albert Hahn im Jahre 1920 fest. Auch spätere Untersuchungen haben seine Beobachtung bestätigt. Zum Beispiel blieb die Sparrate, also die wirkliche psychische Neigung zum Sparen, in den USA zwischen 1951 und 1981 trotz den zahlreichen Veränderungen in der Fiskalpolitik und den wechselnden konjunkturellen Lagen innerhalb der Bandbreite von 16 bis 18 Prozent. Mit Recht wollte also Keynes den Zinssatz als einen Faktor des Sparens nicht anerkennen. Auch was den Zins betrifft, läst sie also einwandfrei die sprichwörtliche Realitätsfremdheit der Neoliberalen in aller Deutlichkeit erkennen. Es kann nicht sein, was nicht sein darf.
Wir haben den Bereich, wo das Gleichgewicht zwischen Investitionen (I) und Ersparnissen (S) stattfinden kann, in unserem Bild mit einem horizontalen Streifen markiert. Er ist an dem oberen und unteren Rand immer blasser, womit angedeutet werden soll, dass dort die Wahrscheinlichkeit des Gleichgewichts immer geringer wird. Dies würde den empirischen Tatsachen Rechnung tragen. Im Prinzip würden damit sowohl die Angebotstheoretiker als auch die monetären Nachfragetheoretiker - Keynes einschließlich - einverstanden sein. Sie würden aber völlig unterschiedliche Erklärungen dafür bieten. Die Angebotstheoretiker würden als Erklärung die bereits erörterte einfache Zinserklärung vorlegen, die Keynesianer würden auch manche anderen Faktoren berücksichtigen und damit die Erklärung deutlich komplizierter machen. Da aber im Endergebnis dasselbe herauskommen würde, wollen wir uns im Folgenden der angebotstheoretischen Erklärung bedienen. Dies bedeutet zwar eine bewusste Abkehr von der Realität, es wird aber unsere weitere Erklärung des Gleichgewichts und Ungleichgewichts einfacher machen, was uns vorerst viel wichtiger ist. So werden wir uns besser darauf konzentrieren können, was bei der Deutung des Gleichgewichts bzw. Ungleichgewichts in der realen Nachfragetheorie wirklich neu ist.
Der Ausgangspunkt ist in unserem Fall das Gleichgewicht (YK′ = I′ = S′) bei der Preissteigerung von 2%, wo alle drei Größen den Wert 120 haben. Nehmen wir jetzt an, die Inflationsrate verdoppelt sich auf 4%. Dies würde konkret bedeuten, dass der Wert von YK′ auf 240 steigt, wie es die obige gestrichelte Linie zeigt. In der guten konjunkturellen Lage wäre durchaus vorstellbar, dass dann Sparen und Investieren spontan noch zunehmen. Das Kreuz (I′ x S′) würde sich folglich nach oben in Bewegung setzen, und bei besonders günstigen Umständen würde es sogar die jetzt nach oben verschobene Linie erreichen. Die Preissteigerung hätte damit zu mehr Wachstum geführt. Das wäre natürlich nur von Vorteil für die ganze Wirtschaft. Wenn aber keiner bereit wäre, mehr zu sparen und zu investieren, gäbe es diesen zusätzlichen Wachstumsschub zwar nicht, trotzdem müsste im betrachteten Fall nichts Schlimmes passieren. Die Preise würden dann fallen und die gestrichelte Linie einfach absinken, so dass es zum Gleichgewicht auf dem ursprünglichen Niveau kommen könnte. Zusammengefasst: Mit oder ohne Wachstum, es würde sich in diesem Fall die Wirtschaft sozusagen am eigenen Schopf packen und aus dem Ungleichgewicht herausretten.
Nehmen wir jetzt an, dass sich das Gleichgewicht auf dem ursprünglichen Niveau doch nicht stabilisiert hat, weil sich die Preissteigerung verlangsamt hat. Aus welchen Gründen auch immer fiel die Inflation unter 2%. Dies wäre zum Beispiel dann zu erwarten, wenn die Löhne oder Zinsen gefallen sind und die Sektoren dies in ihre Preise einkalkuliert und den Käufern weitergereicht haben. Würden die Preise irgendwann ins Negative übergehen, dann müsste dem auch das Sparen und Investieren folgen - sie müssten dann auch den entsprechenden negativen Wert einnehmen. Wird dies nicht geschehen, weil die Sparer und Investoren dies einfach nicht wollen, kann es sehr gefährlich werden. Die Kluft zwischen der Nachfrage und dem Angebot würde sich immer weiter öffnen und die Wirtschaft würde irgendwann abstürzen.
Man kann hier schon erahnen, dass sich beim Preisverfall etwas abzeichnet, was als Ansatz für die Erklärung der zyklischen Krisen dienen kann. So weit wollen wir jedoch nicht gehen - vorerst nicht. Es wäre nämlich kontraproduktiv, jetzt so weit vorzupreschen, schon deshalb, weil die Preise nicht alleine die Größe YK′ bestimmen. Außerdem muss man noch herausfinden, warum die Preise überhaupt zu sinken beginnen und noch einiges mehr klären. Gerade deshalb werden wir den ökonomischen Zyklen einen eigenen thematischen Bereich widmen. Dort werden wir auf die Ergebnisse unserer Untersuchung zurückgreifen. Aber die Preise bestimmen nicht nur den ökonomischen Zyklus der Marktwirtschaft. Wir erwähnen jetzt nur kurz, was damit gemeint ist, dies näher erörtern werden wir erst später.
Sollten unsere Schlussfolgerungen stimmen, dann würde es bedeuten, dass die Wirtschaft schneller wachsen sollte, wenn die Preise steigen. Dann steigt nämlich auch der Wert von YK′ und dementsprechend wird es möglich, mehr zu sparen und zu investieren. Bei der Preissenkung wird YK′ negativ, was zu einem großen Hindernis für das Zustandekommen des Gleichgewichts wird, weil die Menschen normalerweise nicht geneigt sind, mehr zu konsumieren als sie netto verdienen. Sollten diese theoretischen Ergebnisse richtig sein, sollte man in der Praxis einen Zusammenhang zwischen dem steigenden Preisniveau und der Konjunktur beobachten können. Dieser Zusammenhag war schon am Anfang der kapitalistischen Entwicklung zu beobachten. Einige scharfsinnige Beobachter haben in der Tat bereits damals geahnt, dass die Inflation generell die wirtschaftliche Dynamik fördert. Von den Ökonomen war Pierre Boisguillebert (1646-1714) der erste, der hohe Preise explizit mit einer prosperierenden Wirtschaft in Verbindung gebracht hat. Danach ist viel Zeit vergangen, in der man dies nicht mehr wahr haben wollte, bis die moderne Statistik die Boisguillebertsche Einschätzung als richtig bestätigt hat. Der größten Bekanntheit erfreuen sich bis heute die empirischen Untersuchungen von Arthur W. Phillips, die zeigen, dass es in Großbritannien während eines Zeitraums von etwa 100 Jahren eine starke umgekehrte Beziehung zwischen der Arbeitslosenquote und der Geldlohnsteigerung gab. „Negative Effekte treten nur auf, wenn die Inflation hoch ist“, so Lester C. Thurow neulich. „Man kann sogar argumentieren, daß Kapitalismus am besten bei einer Inflationsrate von ungefähr 2 Prozent pro Jahr funktioniert. Alles darunter führt zu Problemen.“  Die Erfahrungen mit der Inflation bestätigen somit die altbekannte Regel, wonach die fragwürdigen Dinge dieser Welt an ihrer eigenen Natur zu Grunde gehen, die guten jedoch an ihrer Übertreibung. Wir werden in einem der nächsten Beiträge noch mehr empirisches Material anbieten, das unsere Schlussfolgerungen über die Preise überzeugend bestätigt. Die Erfahrungen mit der Inflation bestätigen somit die altbekannte Regel, wonach die fragwürdigen Dinge dieser Welt an ihrer eigenen Natur zu Grunde gehen, die guten jedoch an ihrer Übertreibung. Wir werden in einem der nächsten Beiträge noch mehr empirisches Material anbieten, das unsere Schlussfolgerungen über die Preise überzeugend bestätigt.
|
|
|
| |
|
|
|
|