Mögen die Beispiele dafür, wie kläglich die atomistische bzw. Pars-pro-toto-Denkweise oder Methode in der Praxis versagt, auch noch so zahlreich sein, relevant müssen sie trotzdem nicht sein. Eine Methode, die universal anwendbar wäre, gab es nämlich noch nie und es wird sie auch nie geben, so dass es nicht so wichtig ist, was eine Methode nicht kann, sondern alleine das, was sie kann. Folglich wäre es voreilig zu verlangen, die neoliberale Theorie schon deshalb zu verwerfen, weil sie sich einer in der Wissenschaft schon längst überholten Methode bedient. Außerdem darf man nicht außer Acht lassen, dass sich gerade diese Methode wie kaum eine andere um die Entstehung der klassischen Mechanik bzw. Physik, also der ersten exakten Wissenschaft, verdient gemacht hat. An sich betrachtet, ist also die Pars-pro-toto-Methode bzw. -Denkweise nicht unbedingt und immer falsch. Deshalb können über ihre Richtigkeit und Brauchbarkeit in der ökonomischen Theorie alleine ihre konkreten Ergebnisse entscheiden.

Beruht aber die neoliberale Theorie wirklich auf der Pars-pro-toto-Denkweise bzw. auf der atomistischen Vorstellung von der Realität, die man der klassischen Physik abgeguckt hat? Davon will man schon seit geraumer Zeit nichts mehr hören. Seitdem nämlich die klassische Physik oder genauer gesagt ihre atomistische Auffassung der Wirklichkeit endgültig und unwiderruflich ins Museum verabschiedet wurde, will kein neoliberaler Ökonom mehr etwas davon wissen, dass es Dampflockingenieure waren, die durch ihr Gleichgewichtsmodell eine partikel-mechanische Auffassung der Marktwirtschaft theoretisch realisierten, und dass sie unheimlich stolz darauf waren, die damalige (klassische) Mechanik nachahmen zu können. Seitdem wird das Gleichgewichtsmodell bzw. die ganze Theorie, die auf ihm beruht, als eine, auf mathematischen Methoden aufgebaute abstrakte Erklärung der Funktionsweise der Marktwirtschaft präsentiert. Man tut dabei so, als ob es eine „neutrale“ Mathematik gäbe, die sich notwendigerweise auf die „objektive“ Welt bezieht, und Walras - wenn man ihn überhaupt noch erwähnt - wird als ein mathematisch denkender Ökonom dargestellt, der herausgefunden hat, wie man diese Mathematik in der ökonomischen Theorie nutzen kann.

Eine „neutrale“ Mathematik, die sich notwendigerweise auf die „objektive“ Welt bezieht, gibt es aber nicht. Wenn ein mathematischer Wissenschaftler einen Bereich der Wirklichkeit erforscht, bedient er sich nicht der Mathematik, sondern einer bestimmten, sehr kleinen Anzahl (Untermenge) ihrer Methoden oder Techniken. Deshalb sagt man auch, die Mathematik sei ein Werkzeugkasten, aus dem man das wähle, was man in einer bestimmten Situation brauche. Wir werden noch ausführlicher darüber sprechen, was die Mathematik bedeutet und wozu sie nützlich ist.

Außerdem steht am Anfang einer Theorie bzw. eines Modells (Paradigma) nicht die Mathematik, sondern eine Idee oder Vision. So ist es in den exakten Wissenschaften und auch in den Wirtschaftswissenschaften kann es nicht anders sein. Die Mathematik, der sich die neoliberalen Ökonomen bedienen, ist auch nur eine Mathematik, die einem spezifischen Zweck dient: eine bestimmte Auffassung zu interpretieren, konkret eine über den atomistischen Aufbau der (untersuchten) Wirklichkeit. Und weil dem gerade so ist, wird es den neoliberalen Ökonomen nie gelingen, die wahren Hintergründe ihrer Theorie bzw. ihres Gleichgewichtsmodells zu verbergen. Die Mathematik wird sie immer als Nachahmer der mechanischen bzw. atomistischen Sichtweise der Welt verraten.

Nein, lieber Leser, du brauchst keine Angst zu haben. (Auch wenn du mehr oder weniger schon immer die Mathematik heimlich gehasst hast, macht nichts.) Wir werden in allen folgenden Erklärungen und Analysen so vorgehen, dass wir auf die mathematischen Details, also auf die mathematischen Methoden und Techniken verzichten. Konkret wird es so aussehen: Wir beschreiben das ökonomische Problem und die Vorstellung, wie man es mathematisch zu lösen versuchte. Dann sagen wir, (1) was sich mit der Mathematik tatsächlich erreichen ließ und (2) was man von dem mathematischen Ergebnis halten kann.

Wir fangen mit Walras an, bzw. mit seinem bahnbrechenden Buch Mathematische Theorie der Preisbestimmung der wirtschaftlichen Güter. Dort beginnt er den Bau seines Gleichgewichtsmodells mit zwei Marktsubjekten, die zwei Güter, Hafer und Weizen, tauschen wollen. Damit hat er zugleich auch die Entscheidung getroffen, was als der elementare Teil seines Systems des Tausches gelten soll, nämlich das Individuum mit seinen Präferenzen, die sich auf die zum Tausch stehenden Güter (kausal) beziehen. Bei Walras sind diese Güter eben Hafer und Weizen. Warum gerade sie? In der damaligen Welt, die noch weitgehend ländlich war, dürfte das Beispiel eines Warenaustauschs zwischen Bauern vielleicht die beste Wahl gewesen sein. Trotzdem hat dieser Tausch nichts Besonderes an sich. Er entspricht dem Vorgehen in unserem Gefangenenlager, z.B. dem Tausch von Würstchen und Milchdosen zwischen dem Milchtrinker und Würstchenesser . Deshalb weichen wir jetzt auf dieses Tauschbeispiel aus. Dort lassen sich nämlich die Präferenzen der Tauschakteure besser erkennen und verstehen.

Was kann man über die Präferenzen des Milchtrinkers sagen? Wenn er gern Milch trinkt, werden ihm die 10 Milchpulverdosen nicht reichen, so dass er durch Tausch versuchen wird, an mehr Milchpulverdosen zu kommen. Wenn es für ihn gut geht, wird er nach dem Tausch mehr als 10 Milchpulverdosen besitzen. Diese einfache Schlussfolgerung muss natürlich als Ergebnis auch aus dem Walrasschen Modell des Tausches folgen. Wäre man jedoch mit Hilfe dieses Modells nur im Stande diese offensichtliche Schlussfolgerung analytisch bzw. mathematisch „streng“ zu bestätigen (was auch immer dies zu bedeutet hat), wäre das ganze Walrassche mathematische Unterfangen nichts mehr als eine theoretische Übung - ein Spiel. Sich mit Hilfe von Mathematik zu einer Schlussfolgerung durchzukämpfen, die man auch ohne sie schon kennt, könnte zwar einem leidenschaftlichen Mathematiker Vergnügen bereiten, aber von einem wissenschaftlichen Fortschritt könnte noch keine Rede sein. Das Modell von Walras kann in der Tat mehr, und zwar etwas, wofür unser Beispiel des Tausches zwischen den Gefangenen völlig ungeeignet ist:

1) Aus unserem Musterbeispiel wäre es unmöglich herauszufinden, wie viele Milchdosen genau „über die Theke“ gehen würden.

2) Ebenfalls ließe sich nicht herausfinden, welche Tauschverhältnisse sich zwischen den Gütern im Gefangenenlager herausbilden würden.

Das Walrassche Modell, das beide Aufgaben lösen kann, beruht auf dem Prinzip des abnehmenden Nutzens. Dieses Prinzip, das auch als Gesetz des abnehmenden Grenznutzens bezeichnet wird, ist also die tragende Säule der neoliberalen ökonomischen Theorie.

Wer aber jetzt einfach schließen würde, die neuen (neoklassischen) Liberalen seien diejenigen gewesen, die dieses „Gesetz“ entdeckt haben, würde falsch liegen. Was die Neoliberalen feierlich auf das Niveau eines „Gesetzes“  erhoben haben, ist weder neu noch originell. Außerdem steht dieses „Gesetz“ für ganz gewöhnliche Tatsachen, deren sich jeder von uns mehr oder weniger bewusst ist: Es ist also eine Trivialität aus dem Alltagsleben. Wenn man den neoliberalen Ökonomen überhaupt etwas als Verdienst anrechnen sollte, dann nur, dass sie für eine uralte und banale Beobachtung, die zugleich so selbstverständlich ist, dass sie schon immer und überall zu dem alltäglichen praktischen Wissen gehörte, eine geschickte Formulierung gefunden haben. Deshalb ist unser Musterbeispiel auch gut geeignet, um zu erklären, worum es bei dem abnehmenden Grenznutzen geht.

Wenn wir davon ausgehen, dass es in unserem Gefangenenlager zuerst keine Milch gab, ist dies für unseren Milchtrinker bestimmt eine harte Zeit gewesen. Als er dann später 10 Milchpulverdosen pro Monat bekommen und sich noch einige mehr durch den Tausch erworben hat, hat sich seine Lage deutlich verbessert. Wir wollen aber seine Verfassung und sein Verhalten genauer erforschen. Nehmen wir im ersten Schritt an, die wohltätige Organisation hätte den Gefangenen nur 1 Milchpulverdose pro Monat gespendet. Unser Milchtrinker würde sich dann sehr sorgfältig überlegen, wie er den Inhalt dieser einen Dose konsumieren sollte. Wahrscheinlich würde er jeden Tag ein Löffelchen Milchpulver nehmen, um für sich ein paar Schlücke Milch herzustellen. Wir können uns vorstellen, mit welchem Genuss er diese paar Schlucke trinken würde - wie „nützlich“ sie für ihn sein würden. Wir haben im nächsten Bild diesen seinen Nutzen mit einem Balken dargestellt, genauer gesagt dem ersten von links.

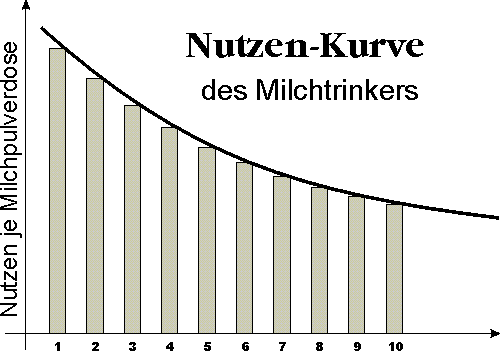
Wenn er zwei Milchdosen hätte, könnte er jeden Tag schon doppelt so viel Milch trinken. Sein Bedürfnis nach Milch würde er also ein bisschen besser befriedigen können, so dass auch seine Befriedigung von Milchtrinken nicht so groß sein wird wie früher. Deshalb ist der Balken 2 in unserem Bild kleiner. Wenn der Milchtrinker 3, 4 und mehr Mildchosen hätte, wäre für ihn das Milchtrinken immer weniger zu einem besonderen Ereignis und Genuss. Der Nutzen jeder zusätzlichen Milchdose verringert sich also für ihn.

Verbindet man die Spitzen der Balken unseres Diagramms mit einer Linie bzw. Kurve, bekommt man eine Figur, die man aus der Mathematik gut kennt. Mit solchen Kurven werden mathematische Funktionen graphisch dargestellt. In diesem Sinne könnten wir in unserem Fall sagen, dass der Nutzen (y-Achse) eine Funktion der konsumierten Menge (x-Achse) ist. Die Beziehung zwischen zwei Quantitäten mathematisch auszudrücken ist natürlich nichts Besonderes und schon gar nicht etwas Neues. Wenn man aber etwas als eine mathematische Funktion interpretiert, muss dies einen Sinn haben, sonst ist es wissenschaftlich betrachtet wertlos. Hat es nun wirklich einen Sinn, die ökonomischen Größen bzw. die Beziehungen zwischen ihnen durch mathematische Funktionen darzustellen?

Die älteren Ökonomen haben darin noch keinen Sinn gesehen. Sie wussten die Mathematik zwar zu schätzen, aber nur wenn es darum ging, die empirischen bzw. statistischen Daten zu erfassen und zu bearbeiten. Für eine solche „politische Arithmetik“ hat sich bereits William Petty (1623 - 1687), ein britischer Ökonom, Wissenschaftler und Philosoph, stark eingesetzt. Aber für eine andere Anwendung der Mathematik zeigten die älteren Ökonomen kein Verständnis und folglich auch kein Interesse. Erst Augustin Cournot (1801-1877) hatte eine Vorstellung davon, wie die Mathematik auch anders anzuwenden wäre. Er meinte, mit mathematischen Mitteln das praktische Verhalten der Monopole bzw. der Oligopole erklären zu können. Dazu hat er eine stetige und monoton fallende Funktion benutzt. Diese Funktion sieht also nicht viel anders aus als diejenige in unserem vorigen Bild. Die Cournotschen Untersuchungen: Recherches sur les principes mathématiques de la théorie des richesses, die heute als das Pionierwerk der mathematischen ökonomischen Theorie gepriesen werden, sind im Jahre 1838 erschienen, sind aber zu dieser Zeit weitgehend unbeachtet geblieben. Cournot vereinfachte sie daher und veröffentlichte sie später (1863 und 1876) erneut, trotzdem hat er kaum jemanden überzeugen können.

Cournot studierte Mathematik und wurde später Professor für Mathematik in Lyon. Sein Vorschlag, eine ökonomische Größe (bei ihm war es die Nachfrage) mit einer stetigen und monoton fallenden Funktion darzustellen, sollte helfen, einzelne konkrete Probleme mathematisch bzw. geometrisch zu lösen. Walras wollte Ingenieur werden, so dass die Mathematik, die er während seiner Studien kennen lernte, eine etwas andere war: Es war eine Mathematik, mit der sich mechanische Systeme mit beliebig vielen Komponenten (Partikeln) modellieren lassen. Diese mathematische Konzeption der klassischen Mechanik wurde für Walras zum Vorbild, wie man auch den Markt als ein System erfassen und erforschen sollte.

Es gibt viele unterschiedliche mechanische Systeme, aber die paradigmatischen Begriffe für sie alle sind schon bei der Untersuchung der Bewegung der freien Himmelskörper entworfen worden. Der Himmel war sozusagen der Geburtsort der klassischen Physik. Die Aufgabe, die sich die ersten Physiker gestellt haben, bestand darin, herauszufinden, wie sich die himmlischen Körper unter der Wirkung der Kräfte bewegen. So ist die Gravitationskraft bzw. die Kraft im Allgemeinen zu einer der wichtigsten Größen der mechanischen Systeme geworden. Sie ist ein Begriff für die Bezeichnung der unerklärlichen Wirkungen, die unsichtbar und immateriell sind. Weil die Gravitationskraft die allgegenwärtigste mechanische Kraft unserer Erfahrung ist, bleiben wir auf sie beschränkt. Um die Wirkung der mechanischen Gravitationskraft zu verdeutlichen, nehmen wir zuerst an, wir haben einen Raum mit nur zwei Körpern bzw. Massen, so wie es das nächste Bild zeigt. Die Stärke dieser Kraft zwischen ihnen ist als Kurve dargestellt.

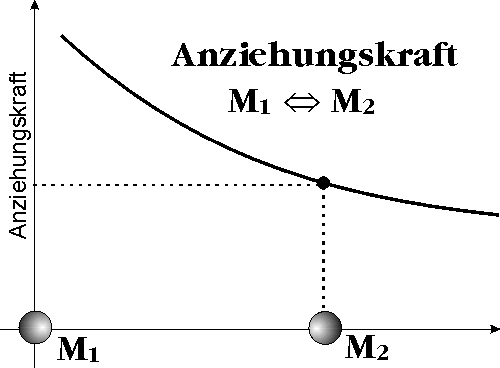
Die Masse M1 stellten wir ins Zentrum des Koordinatensystems, so dass sie als Bezugspunkt des Systems gilt; die andere Masse M2 kann sich entlang der horizontalen Achse frei bewegen. Je weiter die Masse M2 von der Masse M1 positioniert ist, desto schwächer wirkt die Kraft, mit der sie sich anziehen. Wir haben hier also eine stetige und monoton fallende Funktion, die offensichtlich sehr an die (Nachfrage-)Funktion erinnert, mit der sich Cournot beschäftigte. Wenn diese Anziehungskraft bzw. Funktion bekannt ist, lässt sich die Bewegung der Masse M2 genau bestimmen bzw. ausrechnen. Konkret:

Wenn z.B. die Masse M2 am Anfang 1 km vom Koordinatenzentrum entfernt ist und ruht (der einfachere Fall), kann der Physiker genau ausrechnen, um wie viel Meter sie sich nach 1 Sekunde verschiebt.

Die Güter, mit denen sich die ökonomische Theorie beschäftigt, werden auch als Folge des Tausches von einer zur anderen Stelle verschoben (transportiert). Sie bewegen sich also durch den Raum (d.h. werden transportiert), aber dieser Raum an sich ist beim Tausch völlig bedeutungslos. Folglich kann auch die physikalische Maßeinheit Meter für die ökonomische Theorie keine Bedeutung haben. Sollte man daraus folgern, dass die Mathematik, die für die mechanische Bewegung vorgesehen war, für eine andere Bewegungsart ungeeignet wäre? Nein. Für die Mathematik ist es unerheblich, mit welchen Einheiten etwas gemessen wird. Sie kennt eigentlich keine Maßeinheiten:

2 plus 3 kann in der Mathematik immer nur gleich 5 sein, egal ob wir neben diesen Zahlen noch Buchstaben wie m, m/s, kg, °C oder was auch immer schreiben würden.

Für die Mathematik ist ebenfalls unerheblich, ob man das Ergebnis, das sie liefert, abschließend und nachträglich als Raumbewegung unter der Wirkung der mechanischen Kraft oder etwa als Mengenbewegung unter der Wirkung der psychischen Präferenzen interpretiert wird. Dies bedeutet, dass es prinzipiell möglich sein muss, die Situationen, welche durch die Wirkung der Präferenzen (unser erste Bild) auf dem Markt verursacht wird, mit einer gleichen mathematischen Funktion (Kurve) zu erfassen, welche die Bewegung der Körper im Raum beschreibt (das zweite Bild). Es war aber nicht Walras derjenige, dem diese Ähnlichkeit zuerst aufgefallen ist. Die Idee, die Nutzenfunktion ähnlich wie eine mechanische Kraft zu behandeln wurde schon lange vorher geboren, nur sie kam zu früh, als sie dem Zeitgeist noch nicht entsprochen hatte. Gemeint sind die Gedanken von Hermann Gossen (1810-1858) und seine Formulierung der sogenannten „Gossenschen Gesetze“. Nebenbei bemerkt: Gossen hatte die Bedeutung seiner Theorie des abnehmenden (Grenz-)Nutzens für die Ökonomie ähnlich eingeschätzt wie die Entdeckung der Gesetze der Planetenbewegungen durch Kopernikus und Kepler für die Astronomie.

Zwei Elemente bilden aber noch kein (richtiges) System. Sie sind jedoch seine sozusagen erste Stufe, weil ein Element bestimmt noch kein System sein kann. Um die Problematik der theoretischen Konzipierung des Systems näher zu erörtern, knüpfen wir an die einfache Konstellation mit zwei Elementen im letzten Bild an. Die Wirkung zwischen ihnen wird durch die Kurve M1 ⇔ M2 quantitativ bestimmt. Nehmen wir weiter an, es gibt noch Massenpartikel M3, M4 und M5 die auch in das System bzw. in den gleichen physikalischen Raum übernommen werden sollen. Es ist kein Problem, für jeden dieser Massenpartikel den funktionalen Zusammenhang in Bezug auf die (Referenz-)Masse M1 herauszufinden, so dass sich daraus Kurven M1 ⇔ M3, M1 ⇔ M4, M1 ⇔ M5 ergeben. Wird man danach alle fünf Massenpartikel in einen Raum stellen, kann prinzipiell einer der zwei Fälle auftreten

1) Die Kurven werden sich gegenseitig dermaßen beeinflussen oder stören, dass sie sich praktisch zerstören.

2) Die Wirkungen von vier Massenpartikel (etwa: M2, M3, M4 und M5) auf eine Bezugsmasse (etwa: M1) werden sich nur summieren.

Den ersten Fall werden wir etwa in der Chemie haben, wo die (meisten) Eigenschaften der Elemente, die in eine chemische Reaktion treten, in der neu entstandenen Substanz nicht mehr vorhanden sind. (Wenn z.B. Wasserstoff und Sauerstoff als Gase verbrennen, entsteht eine Flüssigkeit: Wasser.) Man kann also in der Chemie von einem qualitativen Umschlag sprechen. Die Physiker haben aber herausgefunden, dass sie solche (prinzipiell unerklärlichen) Probleme nicht haben, dass also bei ihnen der zweite, einfachere Fall eintritt: In ihrer Welt gibt es keine qualitativen Umschläge, sondern nur quantitative Änderungen. Man bezeichnet die auch als Superpositionsprinzip. Die Welt der (klassischen) Mechanik ist also vorbildlich atomistisch und summativ. Es gibt nichts, was im Ganzen (Toto) existiert, was nicht schon in seinen Teilen (Pars) vorhanden war. Und wie ist die Welt der Wirtschaft? 

Auch Walras entschied sich für die Annahme, die Nachfrage- bzw. Nutzenkurven würden sich gegenseitig nicht stören, sondern ihre Wirkungen würden sich nur auf einfache Weise addieren (oder subtrahieren). Walras war der erste, der auf diese Idee kam. Betrachtet man dies als eine rein intellektuelle Errungenschaft, verdient sie bestimmt große Anerkennung. Auf solche Ideen muss man erstmal kommen. Dies war die eindeutige und definitive Entscheidung für die atomistische Weltsicht und die Pars-pro-toto-Methode in der liberalen Wirtschaftstheorie. Die Welt des Tausches, so wie man sie sich in der neoliberalen Theorie vorstellt, wurde damit für immer zu einem Abklatsch der partikel-mechanischen Welt der klassischen Physik.

Das neue mathematische Modell in der ökonomischen Theorie sollte Grundlage sein, auf der man sich erhoffte, eine exakte Wissenschaft aufbauen zu können. Heute, nach mehr als einem Jahrhundert, kann man mit Sicherheit sagen, dass die Arbeiten von Walras und Pareto die Wirtschaftswissenschaft nicht auf den Weg der exakten Wissenschaft geführt haben, sondern in eine Sackgasse. Schlimmer noch! Schon Walras und Pareto haben das Ende dieser Sackgasse erreicht. Es gab also keinen Fortschritt auf den Grundlagen des Gleichgewichtsmodells, so dass wir die neoliberale Theorie schon mit Arbeiten von Walras und Pareto (fast) vollständig erklären können. Die heutige ökonomische Mainstreamtheorie wurde also im Grunde am Ende des 19. und Anfang des 20. Jahrhunderts endgültig axiomatisiert und ausformuliert, so dass sie eine erschreckend vergreiste Wirtschaftstheorie ist. Unsere Wirtschafs- und Produktionsweise, die auf Mikroprozessoren, Robotern und Nanotechnologien beruht, wird durch eine Theorie gedeutet, die in der Zeit der Postkutsche und Dampflok entstanden ist.

Damit die Ironie perfekt wird, soll noch folgendes hinzugefügt werden: Als die neoliberale Theorie vollendet war, wurde die klassische Physik, deren einfältige Magd sie war, von der neuen Physik für alle Ewigkeit ins Museum verabschiedet. Voraussichtlich findet man keinen weiteren Fall, wo die Geschichte einer „Wissenschaft“ so grotesk mitgespielt hat. Die liberale Theorie wollte wissenschaftlich werden, indem sie sich ausgerechnet einer Wissenschaft in den Schoß warf, die sich als falsch erwiesen hat. Dies muss man der neoliberalen Theorie immer wieder aufs Auge drücken. Was soll bitte der ständig heruntergebetete Unsinn: neu, modern oder gar postmodern?

Weil sich aber die neoliberale Theorie als Wissenschaft präsentiert, und dies mit einem - in politischer und ideologischer Hinsicht - wirklich überwältigenden Erfolg, müssen wir uns überwinden und so tun, als ob sie wirklich eine ernsthafte Wissenschaft wäre, und sie auch als solche behandeln. Wir müssen uns also mit ihr, wohl oder übel, mit wissenschaftlichen Argumenten auseinandersetzen. Im Folgenden soll kurz angedeutet werden, auf welchen ökonomischen Bereichen und mit welchen Themen wir dies tun werden.
 

• Die Jagd nach dem Phantom der Preise - Die Beschäftigung mit einem falschen Problem

An der mathematischen Ausformulierung des partikel-mechanischen Modells haben seit Galileo Galilei (1564 - 1642) zahlreiche Mathematiker gearbeitet. Walras stand ihre ganze Erfahrung zur Verfügung, und er wusste, wie er sie sich zunutze machen wollte. Zum Schluss bekam er ein Modell des Tausches, mit dem sich für einen hypothetischen Markt ausrechnen lässt, (1) wie viele Güter sich zu den einzelnen Präferenzquellen bewegen werden und (2) nach welchen Verhältnissen diese Güter getauscht werden. Im Rahmen dieses Modells lassen sich also diejenigen Aufgaben erledigen, für welche wir bereits gesagt haben, dass sie sich im Rahmen unseres Musterbeispiels nicht erledigen lassen.

Die erste Aufgabe des Walrasschen Gleichgewichtsmodells, die Bewegung der Güter durch die Marktkräfte (Präferenzen) quantitativ zu bestimmen, lässt sich auch ohne mathematische Vorkenntnisse verständlich machen. Wir verdeutlichen dies in unserem nächsten Beitrag. Der Hauptakteur ist dort der Milchtrinker aus unserem Musterbeispiel. Seine Präferenz (Vorliebe, Lust, Genuss, ...) für Milch haben wir schon oben mit einer Kurve dargestellt. Sind auch noch seine Präferenz für Würstchen bekannt, lässt sich genau herausfinden, wie viele Würstchen er für Milchpulverdosen austauschen wird, und zwar ohne dass wir dazu komplizierte mathematische Techniken bemühen. Deshalb sollte unser Beispiel im nächsten Beitrag auch für alle, die interessiert sind und ein bisschen Zeit dafür zur Verfügung haben, verständlich sein .

Die zweite Aufgabe, die Bestimmung der Preise, lässt sich ohne Mathematik nicht erledigen und auch nicht einfach erklären. Man muss bestimmte mathematische Vorkenntnisse davon haben, wie ein mathematisches System von Gleichungen entworfen wird und wie man zu Lösungen kommt, welche bei dem neoliberalen Gleichgewichtsmodell die Preise der Güter sind. Deshalb wollen wir uns mit der Bestimmung der Preise nicht näher beschäftigen. Wir bemerken dazu nur, dass ein mathematisches Modell zu entwerfen, mit dem sich die Preise ausrechnen lassen, zweifellos eine großartige intellektuelle Errungenschaft ist, die gelobt und bewundert werden darf. Wie schade, dass das Modell von Walras nur eine reine theoretische Errungenschaft ist. Mit ihm lässt sich nicht ein einziges praktisches Problem lösen.

Das Walrassche Modell kann also nicht dazu dienen, vorherzusagen, wie hoch die Preise bestimmten konkreten Gütern morgen sein werden. Dafür war es auch nicht vorgesehen. Mit ihm sollte man sozusagen das Wesen der Preise erklären, und zwar auf die folgende Weise:

Wie eben gesagt, die Lösung der mathematischen Gleichungen des Gleichgewichtsmodells ergibt die Preise der getauschten Güter. Wenn man die Preise einmal bestimmt hat, kann man testen, was mit dem Preis eines Guts geschieht, wenn sein Angebot kleiner bzw. größer wird. Testet man die Preise in dem Modell von Walras, kommt man zur Schlussfolgerung: Wenn es weniger Güter auf dem Markt gibt, wenn diese also seltener angeboten werden, steigt ihr Preis und umgekehrt. Auf diese Weise meinte Walras das Geheimnis der Preise endgültig lüften zu können. So schreibt er:

„Die Markt- oder Gleichgewichtspreise sind gleich den Quotienten der Seltenheiten.“

...

„Die Tauschwerthe sind proportional den Seltenheiten.“

...

„Wenn mathematisch bewiesen ist; dass die Seltenheit und der Tauschwerth zwei sich begleitende und proportionale Phänomene sind, so ist auch mathematisch bewiesen, dass die Seltenheit die Ursache des Tauschwertes ist.“

Dies nachzuweisen war eigentlich das Hauptanliegen von Walras, was schon aus dem Titel seines Buches unmittelbar ersichtlich wird (Mathematische Theorie der Preisbestimmung der wirthschaftlichen Güter). Warum gerade die Preisbestimmung für ihn von größter Bedeutung war, lässt sich schnell herausfinden.

Schon Adam Smith hat sich für die Preiserklärung interessiert und erst recht die Generation nach ihm. Aber ein anderer Grund dafür, warum die Preiserklärung zu einem so wichtigen Thema wurde, vielleicht das wichtigste im ganzen 19. Jahrhundert, war ein anderer. Marx hat seit Mitte des 19. Jahrhunderts für eine große Unruhe in der Wirtschaftswissenschaft gesorgt, als er mit seiner Arbeitswertlehre mathematisch (arithmetisch) „nachgewiesen“ hat, dass Preise ein Ergebnis von Arbeit sind. Im Lichte dieser Lehre standen die Reichen bzw. die Kapitalisten als reine Ausbeuter und Parasiten der Gesellschaft da. Dass dies den Reichen bzw. den Kapitalisten wenig gefallen hat, lässt sich unschwer nachvollziehen. Es war also für die Herrschenden der industriellen Klassengesellschaft von existentieller Bedeutung, eine Alternative zur Marxschen Theorie aufzustellen, die ihren Reichtum bzw. die Profite moralisch rechtfertigt und verteidigt.

An diesem, sozusagen, „Wettbewerb“ der Preistheorien im 19. Jahrhundert hat sich nun auch Walras beteiligt. Seine Theorie konnte zuerst kaum jemanden überzeugen, weil aber nichts Besseres in Sicht war, musste das liberale Lager wohl oder übel seine Preistheorie doch zum Stein der Weisen erklären. So begann der viele Jahrzehnte andauernde Krieg zwischen Arbeit und Seltenheit (später zum Grenznutzen umbenannt) in der ökonomischen Theorie. Folglich hat sich die ganze Wissenschaft mit falschen Problemen beschäftigt. Deshalb brauchen wir den Preisen nicht viel Aufmerksamkeit zu schenken. Nur noch einmal werden wir die Preisproblematik kurz streifen, bei der Gegenüberstellung der Planwirtschaft und der Marktwirtschaft. Es kann aber mit einigen Worten kurz beschrieben werden, zu welchem konkreten Erkenntnis uns die Preistheorie von Walras verholfen hat. Eine einfache praxisbezogene Überlegung soll dafür reichen.

Stellen wir uns eine Bäuerin vor, deren mathematische Kenntnisse gerade noch für das Zusammenzählen von einfachen Zahlen und im besten Fall auch für das Multiplizieren ausreichen und die in ihrem Leben nie von der ökonomischen Theorie gehört hat. Wir können mit Sicherheit davon ausgehen, dass diese Bäuerin ganz genau weiß, dass sie, wenn sie auf dem Marktplatz die Karotten als einzige anbietet, einen höheren Preis verlangen kann und diesen auch tatsächlich erzielen wird. Ein Bauer, der genauso minimal mathematisch und ökonomisch gebildet ist, weiß aus Erfahrung, dass in Jahren, in denen die Dürre die Ernte in Mitleidenschaft gezogen hat, landwirtschaftliche Produkte teuer sein werden. Nun beweist die Theorie von Walras streng wissenschaftlich, dass die Bäuerin und der Bauer recht haben. Wow! - kann man dazu nur sagen. Traurigerweise wird diese monumentale Theorie - dies kann man nie oft genug wiederholen - niemals der Bäuerin und dem Bauern sagen können, wie die Preise am nächsten Tag sein werden. Auch dann nicht, wenn man alle neoliberalen Professoren und Experten der Welt anheuern und ihnen die schnellsten Computer zur Verfügung stellen würde. Es wäre also für die Bäuerin und den Bauern vollkommen nutzlos, wenn sie sich die ökonomische Theorie von Walras aneignen würden. Trotzdem war Walras unheimlich stolz darauf, nachweisen zu können, dass die Preise etwas mit der Seltenheit zu tun haben. In einem Brief an seinen Freund Georges Renard schrieb er:

„Man muß wissen, was man macht. Will man kurzfristig ernten, muß man Möhren und Salat anbauen; hat man aber den Ehrgeiz, Eichen zu pflanzen, muß man weise genug sein, sich zu sagen: Meine Nachkommen werden mir diesen Schatten verdanken.“

Wen kann also noch wundern, dass die mathematische Spiegelfechterei von Walras die zeitgenössischen Kollegen vorerst völlig kalt ließ. Sie hegten große Zweifel daran, dass es ökonomisch sinnvoll sei, einen solch gigantischen mathematischen Aufwand zu betreiben, nur um zu einem dermaßen altbekannten und trivialen Ergebnis zu gelangen. Folglich haben sie für einige Zeit diese mathematische „Theorie“ als eine intellektuelle Kuriosität beiseite geschoben. Man konnte zwar nicht übersehen, dass die neue „Theorie“ für ideologische Manipulationen bestens geeignet ist, also für die Verteidigung der Interessen der reichen Müßiggänger und sozialen Parasiten, aber auch diesbezüglich hat man vorerst keine großen Hoffnungen in sie gesetzt.

Erwähnen wir an dieser Stelle noch, dass es natürlich auch den Ökonomen schon immer klar war, dass der Preis mit der Seltenheit zu tun hat. So hat etwa Étienne Bonnot de Condillac (1714 - 1780), ein französischer Geistlicher, Philosoph und Logiker, behauptet, der Wert eines Gutes hänge davon ab, in welchen Mengen es zur Verfügung steht. Wir erinnern auch an die vielen Diskussionen alter Ökonomen darüber, warum so nützliche Güter wie etwa Wasser umsonst und so nutzlose wie etwa Diamanten teuer sind („das klassische Wertparadoxon“). Keinem von diesen Ökonomen ist es je entgangen, dass dies mit der Verfügbarkeit bzw. Seltenheit zu tun hat, aber keinem von ihnen käme in den Sinn, eine solche Trivialität an die große Glocke zu hängen. Diese Trivialität in eine komplizierte mathematische Sprache einzukleiden und auf diese Weise aus ihr eine große Weisheit zu machen, dazu waren sich die älteren Ökonomen einfach zu schade.

• Die moralische Rehabilitierung des Selbstsuchts - Eine metaphysische (ontologische) Sackgasse

Man kann sich wirklich nur schwer vorstellen, dass die Walrasschen Bemühungen ausreichen würden, um aus dem Gleichgewichtsmodell eine der erfolgreichsten ökonomischen Lehren zu machen. Erst Pareto war derjenige, der für den Durchbruch gesorgt hat, mit seinem „Beweis“, dass die freie Marktwirtschaft spontan und automatisch sowohl den Konsum als auch die Produktion optimiert. Man sagt heute dazu, er habe nachgewiesen, dass der Markt für die effizienteste Allokation von Ressourcen (bzw. Produktionsfaktoren) sorge. Sein „Beweis“ führte also zur „Erkenntnis“, dass sich das Optimum der ganzen Marktwirtschaft spontan und automatisch aus den sich spontan und automatisch optimierten Teilen (pars pro toto) herausbildet. Damit öffnete sich der Weg für den Siegeszug des Prinzips des individuellen Egoismus und der Rücksichtslosigkeit, so dass die neue „Theorie“ auf einen Schlag ideologisch ungemein attraktiv war. Seitdem konnte jeder reiche Schurke sein Gewissen damit beruhigen, dass er alles, was er zusammengerafft hat, auf eine moralisch völlig unbedenkliche und unanfechtbare Weise erworben hat.

Weil das Paretosche Optimum so wichtig für die ganze neoliberale Theorie ist, werden wir uns mit ihm in den folgenden Beiträgen ausführlich beschäftigen und auseinandersetzen. Im ersten Schritt werden wir uns auf die Anwendung des Paretoschen Optimierungskriterium auf dem Markt der Konsumgüter beschränken, im zweiten Schritt werden wir auch die Produktionsgüter in Betracht ziehen. Vorweg können wir dazu Folgendes sagen:

Wie sich schon aus unserem Musterbeispiel (Gefangenenlager) entnehmen lässt, kann der Tausch zwischen rückscihtslosen Egoisten auf dem Konsumgütermarkt in der Tat den individuellen Nutzen maximieren. Das Problem liegt aber darin, dass der Konsumgütermarkt noch keine Wirtschaft ist. Erweitert man das neoliberale Prinzip der Nutzenmaximierung auch auf den Markt der Produktionsgüter (Produktionsfaktoren), entsteht daraus nicht nur ein ideologischer Schwindel in Reinkultur, sondern das Prinzip entpuppt sich als eine akademische Idiotie.

• Der „Gleichgewichtsbeweis“ - Eine misslungene künstliche Befruchtung

Walras wollte mit seinem mathematischen Modell sozusagen zwei Fliegen mit einer Klatsche schlagen: Einerseits die Preise erklären und andererseits den Beweis aufstellen, dass die freie Marktwirtschaft zum Gleichgewicht tendiert. Deshalb bezeichnet er sein Modell als das Modell des allgemeinen Gleichgewichts. Mit dem Gleichgewichtsbeweis wollte er allen Erfahrungen mit den ökonomischen Rezessionen und Depressionen zum Trotz die These glaubwürdig machen, dass die Marktwirtschaft ihrer Natur nach doch nicht krisenanfällig ist, sondern im Gegenteil immer zum Gleichgewicht strebt. Damit sollte ein für allemal klar sein, dass es so etwas wie Marktversagen nicht gibt, dass alles nur auf einer falschen Wahrnehmung beruht.

Wie kam aber Walras auf den Begriff Gleichgewicht? Das Gleichgewicht der Kräfte ist bekanntlich das fundamentale Gesetz der Physik. Deshalb kann uns nicht erspart bleiben, später noch etwas über die Physik zu sagen, um den ökonomischen Begriff „Gleichgewicht“ besser zu verstehen.

• Ein „Totalmodel“ ohne Wachstumstheorie - Ein Löwe endet als Fußabstreicher

Das Gleichgewichtsmodell sollte, wie die Newtonschen drei Gesetze der Mechanik, die Grundlage bilden, auf der sich die Funktionsweise der Marktwirtschaft restlos erklären sollte. Nun ist es so, dass es in diesem Modell, neben vielen anderen Variablen, auch die Variable Zeit nicht gibt. Walras ist es offensichtlich nie eingefallen, wie sich diese wichtige Variable aller physikalischen Modelle in seinem nachgeahmten Modell unterbringen lässt. Wie sollte man aber ohne die Variable Zeit ein Phänomen wie ökonomisches Wachstum, das zweifellos eine zeitliche bzw. historische Dimension hat, erklären?

Die Begründer des Neoliberalismus könnten sich vielleicht noch mit der Hoffnung vertrösten, jemand wird schon irgendwann einfallen, wie man die Zeit ins Gleichgewichtsmodell implementiert. Dies hat sich jedoch als unmöglich erwiesen. Nun musste die ursprüngliche neoliberale Theorie, die auf dem Gleichgewichtsmodell beruht, eine andere Grundlage für die Analyse des ökonomischen Wachstums suchen. Dazu kommen wir auch noch, aber schon vorab kann man folgendes sagen:

Die pars-pro-toto Denkweise ist im Walrasschen Gleichgewichtsmodell in der Tat geschickt hinter einem Haufen von mathematischen Gleichungen versteckt. Deshalb mussten wir, um diese Denkweise zu entlarven, auf die klassische Physik und die antike Atomistik zurückgreifen. Die neoliberale Theorie des ökonomischen Wachstums hat diese Tarnung einfach beiseite geschoben. Sie schreibt eine einzige Gleichung auf, sozusagen eine Zauberformel, in der alle Geheimnisse der Wirtschaft eingeschlossen sind, man muss sich nur clevere mathematische Techniken ausdenken, um diese Zauberformel zum Sprechen zu bringen. Würde man die Walrasschen Spitzfindigkeiten noch verharmlosend als Komödie bezeichnen, dann wäre die viel jüngere neoliberale Wachstumstheorie eine richtige Farce.